题目内容
6．
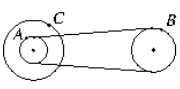如图为一皮带传动装置，大轮与小轮固定在同一根轴上，小轮与另一中等大小的轮子间用皮带相连，它们的半径之比是RA：RB：RC=2：3：4，A、B、C分别为轮子边缘上的三点，那么三点线速度之比vA：vB：vC=1：1：2；角速度之比ωA：ωB：ωC=3：2：3；向心加速度之比aA：aB：aC=3：2：6．
分析 分别研究A与C和A与B之间角速度关系：A、C在同一个轮子上，角速度相等．A、B两点的线速度大小相等，由公式v=ωr，研究两者线速度的关系．根据a=vω判断向心加速度的大小关系．
解答 解：对于A、C两点：角速度ω相等，由公式v=ωr，得：vA：vC=rA：rC=2：4=1：2；
对于A、B两点：线速度大小v相等；所以三点线速度之比：vA：vB：vC=1：1：2；
对于A、B两点：线速度大小v相等，由公式v=ωr，得：ωA：ωB=rB：rA=3：2
综上分析知角速度之比为：ωA：ωB：ωC=3：2：3；
向心加速度：a=ωv
所以：aA：aB：aC=vA•ωA：vBωB：vCωC=1×3：1×2：2×3=3：2：6
故答案为：1：1：2；3：2：3；3：2：6
点评 本题是圆周运动中常见的问题，关键抓住两个相等的物理量：共轴转动的同一物体上各点的角速度相等；两个轮子边缘上各点的线速度大小相等．
练习册系列答案
相关题目
,之后进入电场线竖直向下的匀强电场
发生偏转，最后打在屏上，整个装置处于真空中，不计粒子重力及其相互作用，那么（ ）
对三种粒子做功一样多
14．
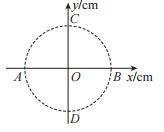如图所示，在真空中xOy平面上，有半径为R=1 cm的圆周，A、B、C、D为圆周上的四个点，若将电荷量均为q=+2.0×10-6 C的两个点电荷分别固定在A、B两点．已知静电力常量k=9.0×109 N•m2/C2，则（ ）
如图所示，在真空中xOy平面上，有半径为R=1 cm的圆周，A、B、C、D为圆周上的四个点，若将电荷量均为q=+2.0×10-6 C的两个点电荷分别固定在A、B两点．已知静电力常量k=9.0×109 N•m2/C2，则（ ）| A． | 两点电荷间的库仑力大小为9.0×10-3 N | |
| B． | C点的电场强度的大小为1.3×108 N/C | |
| C． | C点的场强E的方向沿y轴负方向 | |
| D． | 将一正点电荷从C点移到D点，电场力做负功 |
1．如图所示，某健身爱好者手拉着轻绳，在粗糙的水平地面上缓慢地移动，保持绳索始终平行于地面．为了锻炼自己的臂力和腿部力量，可以在O点悬挂不同的重物C．则（ ）
| A． | 若健身者缓慢向右移动，绳OA拉力变小 | |
| B． | 若健身者缓慢向左移动，绳OB拉力变大 | |
| C． | 著健身者缓慢向右移动，绳OA、OB拉力的合力变大 | |
| D． | 若健身者缓慢向左移动，健身者与地面间的摩擦力变小 |
有一盛满清水的水池，水池深为d，底面能够反光，一束红色激光以45°的入射角Q点射入水中，经底面反射后，从水面上P射出，已知P、Q间的距离为$\frac{2}{3}$$\sqrt{3}$d，真空中的光速为c，求：
等腰三棱镜ABC顶角为120°，AB边长度为16cm，一束单色光平行于底边BC从AB边上的O1点射入三棱镜，在BC边发生全反射后从AC边的O1点射出三棱镜，射到屏上的D点，其中O1、O、O2三点均为对应边的中点，光在真空中的传播速度为3×108m/s．
15．在光电效应实验中，下列表述正确的是（ ）
| A． | 光照时间越长光电流越大． | |
| B． | 饱和光电流的大小与入射光的强度有关 | |
| C． | 遏止电压与入射光的强度有关 | |
| D． | 入射光频率小于极限频率时不能逸出光电子 |
1．
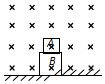某空间存在着如图所示的水平方向的匀强磁场，A、B两个物块叠放在一起，并置于光滑的绝缘水平地面上，物块A带正电，物块B为不带电的绝缘块，水平恒力F作用于物块B上，使A、B一起由静止开始向左运动．在A、B一起向左运动的过程中，以下关于A、B受力和运动的说法中正确的是（ ）
某空间存在着如图所示的水平方向的匀强磁场，A、B两个物块叠放在一起，并置于光滑的绝缘水平地面上，物块A带正电，物块B为不带电的绝缘块，水平恒力F作用于物块B上，使A、B一起由静止开始向左运动．在A、B一起向左运动的过程中，以下关于A、B受力和运动的说法中正确的是（ ）| A． | A对B的摩擦力变大 | B． | B对地面的压力保持不变 | ||
| C． | A对B的压力变大 | D． | B对A的摩擦力保持不变 |