题目内容
18. 等腰三棱镜ABC顶角为120°,AB边长度为16cm,一束单色光平行于底边BC从AB边上的O1点射入三棱镜,在BC边发生全反射后从AC边的O1点射出三棱镜,射到屏上的D点,其中O1、O、O2三点均为对应边的中点,光在真空中的传播速度为3×108m/s.
等腰三棱镜ABC顶角为120°,AB边长度为16cm,一束单色光平行于底边BC从AB边上的O1点射入三棱镜,在BC边发生全反射后从AC边的O1点射出三棱镜,射到屏上的D点,其中O1、O、O2三点均为对应边的中点,光在真空中的传播速度为3×108m/s.(1)求该三棱镜的折射率及光线从O1点传播到O2点所用的时间(时间结果保留一位有效数字);
(2)现把入射光线向下平移至O1B的中点,则光屏上的光斑向哪个方向移动,移动的距离为多少?
分析 (1)由几何关系求出光线在AB界面上的入射角和折射角,再由折射率定义求三棱镜的折射率.由v=$\frac{c}{n}$求得光在三棱镜中的传播速度v,由几何知识求出光线从O1点传播到O2点的路程,再求传播时间.
(2)作出光路图,根据几何知识求光屏上的光斑移动的距离.
解答 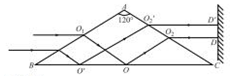 解:(1)由几何关系得光线在AB界面上的入射角 i=60°,折射角 r=30°
解:(1)由几何关系得光线在AB界面上的入射角 i=60°,折射角 r=30°
由折射定律得三棱镜的折射率 n=$\frac{sini}{sinr}$=$\frac{sin60°}{sin30°}$=$\sqrt{3}$
光在三棱镜中的传播速度 v=$\frac{c}{n}$=$\frac{3×1{0}^{8}}{\sqrt{3}}$=$\sqrt{3}×1{0}^{8}$m/s
光在三棱镜中的传播路程 s=O1O+OO2=AB=16cm=0.16m
所以光线从O1点传播到O2点所用的时间 t=$\frac{s}{v}$=$\frac{0.16}{\sqrt{3}×1{0}^{8}}$s≈9×10-9s
(2)把入射光线向下平移至O1B的中点,折射光线向左平移,O′点为BO的中点,则 O′C=$\frac{3}{4}$BC,O2′=$\frac{3}{4}$AC
则光屏上的光斑向上移动.
原光路关于AO左右对称,O2C=$\frac{1}{2}$AC
O2′O2=$\frac{1}{4}$AC=4cm
则光屏上的光斑移动的距离 DD′=O2′O2sin30°=4×0.5cm=2cm
答:(1)求该三棱镜的折射率是$\sqrt{3}$,光线从O1点传播到O2点所用的时间是9×10-9s;
(2)现把入射光线向下平移至O1B的中点,则光屏上的光斑向上移动,移动的距离为2cm.
点评 解决本题的关键要要掌握折射定律,灵活运用数学知识帮助分析和计算.

 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案| A. | 滑动摩擦力阻碍物体的相对运动,一定做负功 | |
| B. | 静摩擦力有阻碍物体的相对运动趋势的作用,一定不做功 | |
| C. | 静摩擦力和滑动摩擦力都可能做正功 | |
| D. | 作用力做正功,反作用力一定做负功 |
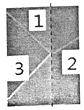 如图是一束白光从一种透明介质进入另一种透明介质的光路图,其中虚线是两种介质的分界线.下列说法正确的是( )
如图是一束白光从一种透明介质进入另一种透明介质的光路图,其中虚线是两种介质的分界线.下列说法正确的是( )| A. | 光线1是入射光,光线2是反射光,光线3是折射光 | |
| B. | 光线2是入射光,光线1是反射光,光线3是折射光 | |
| C. | 光线3是入射光,光线1是反射光,光线2是折射光 | |
| D. | 改变入射光线的入射角,在界面上可能发生全反射 |
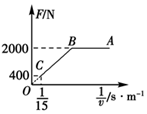 质量为8×102kg的电动车由静止开始沿平直公路行驶,达到的最大速度为15m/s,利用传感器测得此过程中不同时刻电动车的牵引力F与对应的速度v,并描绘出F-$\frac{1}{v}$图象(图中AB、BO均为直线),假设电动车行驶中所受的阻力恒定,则( )
质量为8×102kg的电动车由静止开始沿平直公路行驶,达到的最大速度为15m/s,利用传感器测得此过程中不同时刻电动车的牵引力F与对应的速度v,并描绘出F-$\frac{1}{v}$图象(图中AB、BO均为直线),假设电动车行驶中所受的阻力恒定,则( )| A. | 在全过程中,电动车在B点时速度最大 | |
| B. | AB过程电动车做匀变速运动 | |
| C. | BC过程电动车的牵引力功率不变 | |
| D. | BC过程电动车做减速运动 |
 如图所示,x轴在水平地面内,y轴沿竖直方向.图中画出从y轴上沿x轴正向抛出的三个小球a,b和c的运动轨迹,其中b和c是从同一点抛出的.不计空气阻力,则( )
如图所示,x轴在水平地面内,y轴沿竖直方向.图中画出从y轴上沿x轴正向抛出的三个小球a,b和c的运动轨迹,其中b和c是从同一点抛出的.不计空气阻力,则( )| A. | a在空中运动的时间比b的长 | B. | b和c在空中运动的时间相同 | ||
| C. | a的初速度比b的小 | D. | b的初速度比c的大 |
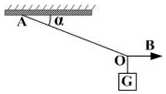 如图所示,一定质量的物块用两根轻绳悬在空中,其中绳OA固定不变,绳OB在竖直平面内由水平方向向上转动,则在绳OB由水平转至竖直的过程中,绳OA的张力和绳OB的张力的大小将( )
如图所示,一定质量的物块用两根轻绳悬在空中,其中绳OA固定不变,绳OB在竖直平面内由水平方向向上转动,则在绳OB由水平转至竖直的过程中,绳OA的张力和绳OB的张力的大小将( )| A. | OA绳的张力一直变大 | B. | OA绳的张力一直变小 | ||
| C. | OB绳的张力先变大后变小 | D. | OB绳的张力先变小后变大 |
 .若灯泡恰能正常发光,则:
.若灯泡恰能正常发光,则:
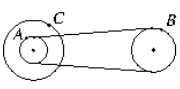 如图为一皮带传动装置,大轮与小轮固定在同一根轴上,小轮与另一中等大小的轮子间用皮带相连,它们的半径之比是RA:RB:RC=2:3:4,A、B、C分别为轮子边缘上的三点,那么三点线速度之比vA:vB:vC=1:1:2;角速度之比ωA:ωB:ωC=3:2:3;向心加速度之比aA:aB:aC=3:2:6.
如图为一皮带传动装置,大轮与小轮固定在同一根轴上,小轮与另一中等大小的轮子间用皮带相连,它们的半径之比是RA:RB:RC=2:3:4,A、B、C分别为轮子边缘上的三点,那么三点线速度之比vA:vB:vC=1:1:2;角速度之比ωA:ωB:ωC=3:2:3;向心加速度之比aA:aB:aC=3:2:6.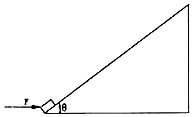 如图所示,水平恒力F=40N作用于一质量m=1kg的小物块上,使小物块由静止开始从倾角θ=37°的固定斜面底端沿斜面上滑,当小物块滑至斜面中点时,撤去F,物块恰好能滑到斜面顶端.(小物块大小可忽略,g=10m/s2,sin37°=0.6,cos37°=0.8),求小物块与斜面间的动摩擦因数μ.
如图所示,水平恒力F=40N作用于一质量m=1kg的小物块上,使小物块由静止开始从倾角θ=37°的固定斜面底端沿斜面上滑,当小物块滑至斜面中点时,撤去F,物块恰好能滑到斜面顶端.(小物块大小可忽略,g=10m/s2,sin37°=0.6,cos37°=0.8),求小物块与斜面间的动摩擦因数μ.