Question

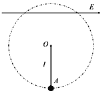
【题目】如图所示，水平面光滑，在虚线的右侧存在场强大小为E，方向向左的匀强电场。一个不带电的小球A恰好静止在虚线与水平面的交点处。电场中，在与A球相距l远处由静止释放一带电量为+q的小球B，经一段时间后A、B发生了弹性正碰。已知A小球的质量为mA，B小球的质量为mB，有mA =2mB。若A、B均为金属小球，形状大小均相同，且可视为质点，不考虑电场边缘效应，求：

(1)碰撞前瞬间B小球的速度；

(2)碰撞后B小球在电场中向右运动的最远距离（已知两小球碰后电量均分，且不考虑小球间的库仑力作用）。

Answer 1

【答案】(1) (2)

【解析】

(1)根据动能定理即可求解B球的初速度；（2）A与B发生弹性碰撞，由动量守恒和能是守恒可求出碰撞后A、B的速度，再根据动能定理可求解B球向右运动的最远距离。

(1)对B球，由出发至即将发生碰撞，根据动能定理有：

解得：

(2)对A、B碰撞过程，设A、B碰撞后速度分别为、

由动量守恒定律有：

由能量守恒定律有：

其中

解得：

对B球，由碰撞至向右到最远，根据动能定理有：

解得：