题目内容
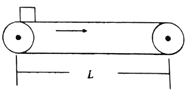
【题目】如图所示,质量为M且足够长的木板静止在光滑水平面上,木板的右侧有一墙壁。一质量为m的物块以速度v0由木板左侧滑上木板,已知物块与木板间的动摩擦因数为,M=3m,木板与墙壁碰撞不损失动能。
![]()
(1)若它们达到共同速度后木板跟墙壁发生碰撞并反弹运动,最终物块能在木板上滑行多少距离?
(2)若要求木板与墙壁能发生第二次碰撞,木板右侧与墙壁间的距离x应满足什么条件?
【答案】(1) ![]() (2)
(2) ![]()
【解析】试题分析:对木板、物块在滑行的过程中运用动量守恒和能量关系,即可求出最终物块能在木板上滑行的距离;根据动量守恒和动能定理结合即可求出木板右侧与墙壁间的距离应满足得条件。
(1)设木板、物块达到的共同速度为![]()
由动量守恒得:![]()
因为:![]() ,解得
,解得![]()
碰撞后,木板原速弹回,由于此时![]() ,可知,最终木板和物块将以共同速度
,可知,最终木板和物块将以共同速度![]() 向左运动
向左运动
由动量守恒得:![]()
解得![]()
设整个运动过程中物块在木板上滑行的距离为L
由能量关系得![]()
代入数值得![]()
(2)设木板碰墙瞬间,物块、木板的速度为![]() ,
,
由动能定理得:![]()
动量守恒得:![]()
若要发生第二次碰撞,要求![]()
木板右侧与墙壁间的距离x应满足![]()

练习册系列答案
相关题目