题目内容
【题目】如图所示，一条长为l的绝缘轻绳上端固定在O点，下端栓一个质量为m，电荷量为+q的小球，将它置于方向水平向右的匀强电场中，当小球平衡时轻绳与竖直方向夹角为37°，不计空气阻力，重力加速度为g（
，
）
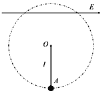
(1)求空间中匀强电场的电场强度E的大小；
(2)在A点给小球一水平向右的瞬时冲量I0，使小球恰能做完整的圆周运动，求I0的大小；
(3)在A点给小球一水平向右的瞬时冲量I（I小于I0）。若小球在之后的运动中恰能通过O点，试求该冲量的大小.
【答案】(1) 
(2) 
(3) 
【解析】
（1）对小球受力分析，根据平衡条件即可求解电场强度E的大小；（2）由等效重力思想求出等效最高点B的速度，再由动能定理求出A点的初速度，根据动量定理即可求出瞬时冲量I0；（3）根据题意，作出小球发生的运动，根据运动学公式、向心力知识和动量定理即可求出该冲量的大小。
（1）由题可得：
，解得：
（2）由等效重力思想，可知当小球通过等效最高点B时，恰由等效重力提供向心力
即：
对A至B过程，由动能定理有：
解得：
由动理定理得：
解得：
（3）设小球在C点脱轨，C点与等效圆心等高的夹角为
，如图所示：
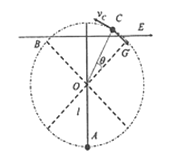
根据运动学公式则有：
，
对C，等效重力沿半径方向的分力恰好提供向心力，则有：
得：
令
，得
，解得：
，即
解得：
故
练习册系列答案
智慧课堂密卷100分单元过关检测系列答案
单元期中期末卷系列答案
相关题目
