题目内容
2.在硏究小车匀变速直线运动规律的实验中,选定一条纸带如图所示,从O点开始,每5个点取一个计数点的纸带.其中0、1、2、3、4、5、6都为记数点.测得:x1=1.40cm,x2=1.90cm,x3=2.38cm,x4=2.88cm,x5=3.39cm,x6=3.87cm.
(1)相邻两计数点之间的时间间隔:T=0.1s
(2)计数点5对应的瞬时速度大小为v5=3.6m/s.(结果保留两位有效数字)
(3)该小车做匀变速直线运动的加速度的表达式为$a=\frac{{x}_{6}-{x}_{1}}{5{T}^{2}}$(用x1、x6和T等表示)
大小a=0.50m/s2.(结果均保留两位有效数字)
分析 根据电源频率与计数点间的间隔数求出计数点间的时间间隔,根据作差法求出加速度,根据匀变速直线运动的推论求出计数点5速度,从而即可求解.
解答 解:(1)源频率为50Hz,打点时间间隔为0.02s,每相邻两个计数点的间还有四点未画出,则每相邻两个计数点的时间间隔T=0.02×5=0.1s.
(2)据匀变速直线运动中间时刻的速度等于平均速度得:
v5=$\frac{{x}_{5}+{x}_{6}}{2T}$=$\frac{0.0339+0.0387}{0.2}$≈3.6m/s,
(3)根据作差法得加速度$a=\frac{{x}_{6}-{x}_{1}}{5{T}^{2}}$
代入数据,解得:a=$\frac{0.0387-0.0140}{5×0.{1}^{2}}$=0.50m/s2,
故答案为:(1)0.1;(2)3.6;(3)$a=\frac{{x}_{6}-{x}_{1}}{5{T}^{2}}$,0.50.
点评 解决本题的关键会通过纸带求解加速度,熟练应用平均速度公式、匀变速直线运动的推论即可正确解题.

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
12.将质量为m的小球以速度v0竖直向上抛出,若不计空气阻力,当小球到达最高点时,它的重力势能增加了( )
| A. | $\frac{1}{4}$m v0 | B. | $\frac{1}{2}$m v02 | C. | m v02 | D. | 2 m v02 |
13.一物体从距离地面H高处自由下落,当其重力势能等于动能的3倍时(以地面为零势能面),物体的速度为( )
| A. | $\frac{1}{2}$$\sqrt{2gH}$ | B. | $\sqrt{gH}$ | C. | $\sqrt{2gH}$ | D. | 2$\sqrt{gH}$ |
17. 如图所示,现有一端固定在地面上的两根长度相同竖直弹簧(K1>K2),两个质量相同的小球分别由两弹簧的正上方高为H处自由下落,落到轻弹簧上将弹簧压缩,小球落到弹簧上将弹簧压缩的过程中获得的最大弹性势能分别是E1和E2,在具有最大动能时刻的重力势能分别是EP1和EP2(以地面为重力势能的零势能),则( )
如图所示,现有一端固定在地面上的两根长度相同竖直弹簧(K1>K2),两个质量相同的小球分别由两弹簧的正上方高为H处自由下落,落到轻弹簧上将弹簧压缩,小球落到弹簧上将弹簧压缩的过程中获得的最大弹性势能分别是E1和E2,在具有最大动能时刻的重力势能分别是EP1和EP2(以地面为重力势能的零势能),则( )
 如图所示,现有一端固定在地面上的两根长度相同竖直弹簧(K1>K2),两个质量相同的小球分别由两弹簧的正上方高为H处自由下落,落到轻弹簧上将弹簧压缩,小球落到弹簧上将弹簧压缩的过程中获得的最大弹性势能分别是E1和E2,在具有最大动能时刻的重力势能分别是EP1和EP2(以地面为重力势能的零势能),则( )
如图所示,现有一端固定在地面上的两根长度相同竖直弹簧(K1>K2),两个质量相同的小球分别由两弹簧的正上方高为H处自由下落,落到轻弹簧上将弹簧压缩,小球落到弹簧上将弹簧压缩的过程中获得的最大弹性势能分别是E1和E2,在具有最大动能时刻的重力势能分别是EP1和EP2(以地面为重力势能的零势能),则( )| A. | E1<E2 | B. | E1>E2 | C. | EP1=EP2 | D. | EP1>EP2 |
14. 如图所示,两条曲线为汽车a、b在同一条平直公路上的速度时间图象,已知在t2时刻,两车相遇,下列说法正确的是( )
如图所示,两条曲线为汽车a、b在同一条平直公路上的速度时间图象,已知在t2时刻,两车相遇,下列说法正确的是( )
 如图所示,两条曲线为汽车a、b在同一条平直公路上的速度时间图象,已知在t2时刻,两车相遇,下列说法正确的是( )
如图所示,两条曲线为汽车a、b在同一条平直公路上的速度时间图象,已知在t2时刻,两车相遇,下列说法正确的是( )| A. | a车速度先减小后增大,b车速度先增大后减小 | |
| B. | t1时刻a车在前,b车在后 | |
| C. | t1~t2时刻a、b的位移相同 | |
| D. | a车加速度先减小后增大,b车加速度先减小后增大 |
12.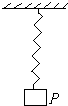 一根轻弹簧,上端固定,下端栓一个重物P,处于静止状态,如图所示.现有外力把它向下拉一段距离,则以下说法正确的是( )
一根轻弹簧,上端固定,下端栓一个重物P,处于静止状态,如图所示.现有外力把它向下拉一段距离,则以下说法正确的是( )
 一根轻弹簧,上端固定,下端栓一个重物P,处于静止状态,如图所示.现有外力把它向下拉一段距离,则以下说法正确的是( )
一根轻弹簧,上端固定,下端栓一个重物P,处于静止状态,如图所示.现有外力把它向下拉一段距离,则以下说法正确的是( )| A. | 向下拉的某段过程中,重力势能的减少量可能大于弹性势能的增加量 | |
| B. | 向下拉的任一段过程中,重力势能的减少量一定小于弹性势能的增加量 | |
| C. | 撤去拉力,P在任一段运动过程中,重力势能的增加量一定等于弹性势能的减少量 | |
| D. | 撤去拉力,P在某段运动过程中,重力势能的增加量可能等于弹性势能的减少量 |
 如图所示,半径为R的光滑金属环竖直放置,环上套有一质量为m的小球,小球开始时静止于最低点.现给小球一冲击,使它以初速度v0沿环上滑,已知v0=$\sqrt{6Rg}$.求:
如图所示,半径为R的光滑金属环竖直放置,环上套有一质量为m的小球,小球开始时静止于最低点.现给小球一冲击,使它以初速度v0沿环上滑,已知v0=$\sqrt{6Rg}$.求: