��Ŀ����
5�� ��ͼ��ʾ��ƽ���ڹ⻬б����ᵯ�ɾ���ϵ��Ϊk��һ�˹̶������Ϊ�ȵ�б��ˣ���һ�������A���ӣ����B��б����������A�ϵ���������⻬б�����봫������öԽӣ������ƽ����ˮƽ�������Ҳ�Ǧȣ�Ƥ������װ��˳ʱ������ת�������A��B������Ϊm����ʼʱ��������ֹ������ƽ����б�����ϵ������������B��ʹB�����ٶ�Ϊa���ȼ����˶���������ڿ�ʼһ��ʱ���ڵ�v-tͼ����ͼ��ʾ��t1ʱ��A��B��ͼ�����У�t2ʱ�̶�ӦAͼ�ߵ���ߵ㣩���������ٶ�Ϊg����t1��t2��v1��v2��δ֪��
��ͼ��ʾ��ƽ���ڹ⻬б����ᵯ�ɾ���ϵ��Ϊk��һ�˹̶������Ϊ�ȵ�б��ˣ���һ�������A���ӣ����B��б����������A�ϵ���������⻬б�����봫������öԽӣ������ƽ����ˮƽ�������Ҳ�Ǧȣ�Ƥ������װ��˳ʱ������ת�������A��B������Ϊm����ʼʱ��������ֹ������ƽ����б�����ϵ������������B��ʹB�����ٶ�Ϊa���ȼ����˶���������ڿ�ʼһ��ʱ���ڵ�v-tͼ����ͼ��ʾ��t1ʱ��A��B��ͼ�����У�t2ʱ�̶�ӦAͼ�ߵ���ߵ㣩���������ٶ�Ϊg����t1��t2��v1��v2��δ֪����1����t2ʱ�̵��ɵ��α䳤��x��
��2����t1��ֵ��
��3����֪��=37�㣬���ʹ������������L=5m������B��Ƥ����Ķ�Ħ��������=0.25����AB�պ���C�㣨б���봫�ʹ������ӵ㣩���벢���봫�����������B�������ʹ���C��ʱ�ٶ�Ϊ8m/s���������Ϊ�ʵ㣬���������B����C��ͬʱ��ȥ����F����sin37��=0.6��cos37��=0.8����������װ������ת�����ٶ�v����v��4m/s�ķ�Χ�ڵ��ڣ����Ƶ�����B����������Dʱ�ٶ�vD�洫�ʹ��ٶ�v�仯�Ĺ�ϵʽ��gȡl0m/s2��
���� ��1��A���ٶ����ʱ���ٶ�Ϊ�㣬���ݺ��˶������A�ﵽ����ٶ�ʱ��λ�ƣ�
��2����ͼ������t1ʱ��A��B��ʼ���룬��A����ţ�ٵڶ����ɺ��˶�ѧ��ʽ���t1��
��3���ִ��ʹ��ٶ���4m/s��v��8m/s��v��8m/s������Χ�������˶�ѧ������ʽ��⣮
��� �⣺��1����ͼ֪��A�ļ��ٶ�Ϊ�㣬�ٶ����
����ţ�ٵڶ����ɺͺ��˶��ɵã�mgsin��=kx���ã�$x=\frac{mgsin��}{k}$
��2����ͼ������t1ʱ��A��B��ʼ���룬��A����ţ�ٵڶ����ɣ�
kx-mgsin��=ma
��ʼʱ�У�2mgsin��=kx0����x0-x=$\frac{1}{2}a{t}_{1}^{2}$
��������ʽ�ã�t1=$\sqrt{\frac{2��mgsin��-ma��}{ak}}$��
��3�������ʹ����ٶ���4m/s��v��8m/s�ķ�Χ�ڵ���ʱ������B���Լ��ٶ�a1�������ϻ���${x}_{1}^{\;}=\frac{{v}_{0}^{2}-{v}_{\;}^{2}}{2{a}_{1}^{\;}}$
���ٶȼ���V������a2�������ϻ���
����B������D��ʱ�ٶ�vD���ٶ�v�ı仯��ϵʽ��${v}_{D}^{\;}=\sqrt{\frac{{v}_{\;}^{2}}{2}-8}$
�����ʹ����ٶ���v��8m/s�ķ�Χ�ڵ���ʱ������B���Լ��ٶ�a2���ٻ��е�D�㣬
${v}_{D}^{2}-{v}_{0}^{2}=-2aL$
����B������D��ʱ�ٶ�vD���ٶ�v�ı仯��ϵʽ�ǣ�${v}_{D}^{\;}=2\sqrt{6}m/s$
�𣺣�1��t2ʱ�̵��ɵ��α䳤��xΪ$\frac{mgsin��}{k}$��
��2��t1��ֵ$\sqrt{\frac{2��mgsin��-ma��}{ak}}$��
��3������B����������Dʱ�ٶ�vD�洫�ʹ��ٶ�v�仯�Ĺ�ϵʽ����4m/s��v��8m/sʱ${v}_{D}^{\;}=\sqrt{\frac{{v}_{\;}^{2}}{2}-8}$����v��8m/sʱ��${v}_{D}^{\;}=2\sqrt{6}m/s$
���� �������Ƕȿ�����������������������������ѹ��Ϊ0�����˶�ѧ�Ƕȿ���һ���˶���������ǡ�÷���ʱ������������б�淽���ϵļ��ٶȺ��ٶ�����ȣ�

| A�� | ����߳�ʱ�������ù��� | |
| B�� | �����϶�δ�ι̵�ϵ�����㣬���г����ɶ���ʹ���߳��������� | |
| C�� | ��ʼ��ʱʱ��������ٰ��� | |
| D�� | ʵ������ 49��ȫ����Ϊ 50�� |
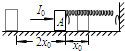 ��ͼ��ʾ������ϵ��Ϊk���ᵯ�ɵ�һ�˹̶���ǽ�ϣ���һ��������ˮƽ��������Ϊm������A�Ӵ�����δ������A���ӣ�����ˮƽ�����α䣮�ֶ�����Aʩ��һ��ˮƽ���ҵ�˲���������СΪI0���������A�����˶���������Ϊx0��֮������A�����ɵ�������ͣ�ھ����ʼλ�����2x0������֪����ʼ���ڵ��ɵ������ڣ�����A��ˮƽ���Ķ�Ħ������Ϊ�̣��������ٶ�Ϊg������˵������ȷ���ǣ�������
��ͼ��ʾ������ϵ��Ϊk���ᵯ�ɵ�һ�˹̶���ǽ�ϣ���һ��������ˮƽ��������Ϊm������A�Ӵ�����δ������A���ӣ�����ˮƽ�����α䣮�ֶ�����Aʩ��һ��ˮƽ���ҵ�˲���������СΪI0���������A�����˶���������Ϊx0��֮������A�����ɵ�������ͣ�ھ����ʼλ�����2x0������֪����ʼ���ڵ��ɵ������ڣ�����A��ˮƽ���Ķ�Ħ������Ϊ�̣��������ٶ�Ϊg������˵������ȷ���ǣ�������| A�� | ����A�����˶����̣����ɶ�����A�ij���Ϊ�� | |
| B�� | ����A�����˶��������뵯�ɽӴ���ʱ��һ����������A�����˶��������뵯�ɽӴ���ʱ�� | |
| C�� | ����A�����˶��������Ekm=$\frac{{{I}_{0}}^{2}}{2m}$-2��mgx0 | |
| D�� | ����A�뵯�����õĹ����У�ϵͳ�����������Ep=$\frac{{{I}_{0}}^{2}}{2m}$-��mgx0 |
| A�� | $\frac{1}{2}$$\sqrt{2gH}$ | B�� | $\sqrt{gH}$ | C�� | $\sqrt{2gH}$ | D�� | 2$\sqrt{gH}$ |
 ��ͼ��ʾ������һ�˹̶��ڵ����ϵ�����������ͬ��ֱ���ɣ�K1��K2��������������ͬ��С��ֱ��������ɵ����Ϸ���ΪH���������䣬�䵽�ᵯ���Ͻ�����ѹ����С���䵽�����Ͻ�����ѹ���Ĺ����л�õ���������ֱܷ���E1��E2���ھ��������ʱ�̵��������ֱܷ���EP1��EP2���Ե���Ϊ�������ܵ������ܣ���������
��ͼ��ʾ������һ�˹̶��ڵ����ϵ�����������ͬ��ֱ���ɣ�K1��K2��������������ͬ��С��ֱ��������ɵ����Ϸ���ΪH���������䣬�䵽�ᵯ���Ͻ�����ѹ����С���䵽�����Ͻ�����ѹ���Ĺ����л�õ���������ֱܷ���E1��E2���ھ��������ʱ�̵��������ֱܷ���EP1��EP2���Ե���Ϊ�������ܵ������ܣ���������| A�� | E1��E2 | B�� | E1��E2 | C�� | EP1=EP2 | D�� | EP1��EP2 |
 ��ͼ��ʾ����������Ϊ����a��b��ͬһ��ƽֱ��·�ϵ��ٶ�ʱ��ͼ����֪��t2ʱ�̣���������������˵����ȷ���ǣ�������
��ͼ��ʾ����������Ϊ����a��b��ͬһ��ƽֱ��·�ϵ��ٶ�ʱ��ͼ����֪��t2ʱ�̣���������������˵����ȷ���ǣ�������| A�� | a���ٶ��ȼ�С������b���ٶ���������С | |
| B�� | t1ʱ��a����ǰ��b���ں� | |
| C�� | t1��t2ʱ��a��b��λ����ͬ | |
| D�� | a�����ٶ��ȼ�С������b�����ٶ��ȼ�С������ |
| A�� | ����������ӵ��˶��������£���ijһʱ�̣������κ�һ�������˶��ķ��Ӷ��У���������������˶������������Ŀ����� | |
| B�� | ������������������˶��������д���С�����Ƿ��ӵ����ʰ����� �� �٣��� ͷ �ࡱ�� �� �ɷֲ� | |
| C�� | ����ѹǿ�Ĵ�С��������ӵ�ƽ�����ܡ����ӵ��ܼ��̶������������й� | |
| D�� | һ��������ij���������壬�¶�����ʱ�����ӵ�ƽ���������������ѹǿһ������ | |
| E�� | �����������ѹǿ�Ǵ���������� ����������ײ����� |
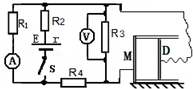 ��ͼ��ʾ��ˮƽ���õ������ڷ����һ���������������壬���IJ��Ϊ�⻬��Ե�壬��M������D��Ϊ���岢�õ��߰�ͼ���ӣ��������S=2cm2������Ͽ�ʱ��DM���l1=5��m���պϵ������D���M�ֱ���е������ֵ�ɣ������Բ�����ǿ�糡��D��M��ĵ糡Ϊ���Բ����ĵ糡�ĵ��ӣ����ڵ糡�������»���D�����ƶ����ȶ���DM���l2=4��m����ʱ����������Ϊ0.75A����ѹ������Ϊ2V����֪R4=4��������ѹǿ��0=1.0��105Pa�������ƶ�ǰ�������¶Ȳ��䣮
��ͼ��ʾ��ˮƽ���õ������ڷ����һ���������������壬���IJ��Ϊ�⻬��Ե�壬��M������D��Ϊ���岢�õ��߰�ͼ���ӣ��������S=2cm2������Ͽ�ʱ��DM���l1=5��m���պϵ������D���M�ֱ���е������ֵ�ɣ������Բ�����ǿ�糡��D��M��ĵ糡Ϊ���Բ����ĵ糡�ĵ��ӣ����ڵ糡�������»���D�����ƶ����ȶ���DM���l2=4��m����ʱ����������Ϊ0.75A����ѹ������Ϊ2V����֪R4=4��������ѹǿ��0=1.0��105Pa�������ƶ�ǰ�������¶Ȳ��䣮