题目内容
2. 如图所示,实线是一列沿x轴传播的正弦波在t1=0时刻的波形图线,虚线是该波在t2=0.5s时刻的波形图线.已知该波的周期T>1s,P质点的坐标是(0.1,0).求:
如图所示,实线是一列沿x轴传播的正弦波在t1=0时刻的波形图线,虚线是该波在t2=0.5s时刻的波形图线.已知该波的周期T>1s,P质点的坐标是(0.1,0).求:(1)波的传播速度大小v;
(2)质点P的位移yp随时间t的表达式.
分析 (1)由于波的传播方向未知,要分析沿+x方向和沿-x方向两种情况分析,根据波的周期性,写出时间与周期关系式,结合条件T>1s,得到周期值,即可求解波速v.
(2)根据波动图象读出振幅和t=0时刻P点的振动方向,即可写出质点P的位移yp随时间t的表达式.
解答 解:(1)由图线可知:
若波沿+x方向传播,有(n+$\frac{3}{4}$)T=t2-t1,(n=0,1,2,3…) ①
若波沿-x方向传播,(n+$\frac{1}{4}$)T=t2-t1,(n=0,1,2,3…) ②
又由①②式结合T>1s,得:波沿-x方向传播,T=2s
由图线可知:λ=0.2m
则波速 v=$\frac{λ}{T}$=$\frac{0.2}{2}$m/s=0.1m/s
(2)由图线可知:A=0.2m
因为波沿-x方向传播,所以 φ=-π
又有:ω=$\frac{2π}{T}$=$\frac{2π}{2}$=π rad/s
可得P点位移随时间的表达式:yP=0.2sin(πt-π)=-0.2sinπt m
答:(1)波的传播速度大小v是0.1m/s;
(2)质点P的位移yp随时间t的表达式为yP=-0.2sinπt m.
点评 本题知道两个时刻的波形,往往要根据空间的周期性或时间的周期性列出波传播距离或周期的通项式,再求特殊值.

练习册系列答案
 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案
相关题目
12.一台发电机产生的电动势的瞬时值表达式e=311sin314tV,下列说法中正确的是( )
| A. | 该发电机转子的转速为50r/s | |
| B. | 该交流电的周期0.02s | |
| C. | 该发电机可接在耐压值为311V的电容器两端 | |
| D. | 该发电机接在总电阻为110Ω的电路中,每秒中发热为440J |
13.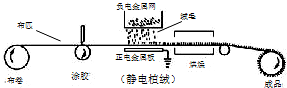 如图,静电植绒时,真空中带负电的绒毛一旦与布匹上的粘合剂接触就粘贴在布匹上,则带负电绒毛落向布匹的过程中( )
如图,静电植绒时,真空中带负电的绒毛一旦与布匹上的粘合剂接触就粘贴在布匹上,则带负电绒毛落向布匹的过程中( )
 如图,静电植绒时,真空中带负电的绒毛一旦与布匹上的粘合剂接触就粘贴在布匹上,则带负电绒毛落向布匹的过程中( )
如图,静电植绒时,真空中带负电的绒毛一旦与布匹上的粘合剂接触就粘贴在布匹上,则带负电绒毛落向布匹的过程中( )| A. | 做匀速运动 | B. | 做加速运动 | C. | 电势能逐渐增大 | D. | 电势能逐渐减小 |
17. 如图所示,一个圆形框架以竖直的直径为转轴匀速转动.在框架上套着两个质量相等的小球A、B,小球A、B到竖直转轴的距离相等,它们与圆形框架保持相对静止.下列说法正确的是( )
如图所示,一个圆形框架以竖直的直径为转轴匀速转动.在框架上套着两个质量相等的小球A、B,小球A、B到竖直转轴的距离相等,它们与圆形框架保持相对静止.下列说法正确的是( )
 如图所示,一个圆形框架以竖直的直径为转轴匀速转动.在框架上套着两个质量相等的小球A、B,小球A、B到竖直转轴的距离相等,它们与圆形框架保持相对静止.下列说法正确的是( )
如图所示,一个圆形框架以竖直的直径为转轴匀速转动.在框架上套着两个质量相等的小球A、B,小球A、B到竖直转轴的距离相等,它们与圆形框架保持相对静止.下列说法正确的是( )| A. | 小球A的合力小于小球B的合力 | |
| B. | 小球A与框架间可能没有摩擦力 | |
| C. | 小球B与框架间可能没有摩擦力 | |
| D. | 圆形框架以更大的角速度转动,小球B受到的摩擦力一定增大 |
14. 如图所示,a、b两小球分别从半圆轨道顶端和斜面顶端以大小相等的初速度v0同时水平抛出,已知半圆轨道的半径与斜面竖直高度相等,斜面底边长是其竖直高度的2倍,若小球a能落到半圆轨道上,小球b能落到斜面上,则( )
如图所示,a、b两小球分别从半圆轨道顶端和斜面顶端以大小相等的初速度v0同时水平抛出,已知半圆轨道的半径与斜面竖直高度相等,斜面底边长是其竖直高度的2倍,若小球a能落到半圆轨道上,小球b能落到斜面上,则( )
 如图所示,a、b两小球分别从半圆轨道顶端和斜面顶端以大小相等的初速度v0同时水平抛出,已知半圆轨道的半径与斜面竖直高度相等,斜面底边长是其竖直高度的2倍,若小球a能落到半圆轨道上,小球b能落到斜面上,则( )
如图所示,a、b两小球分别从半圆轨道顶端和斜面顶端以大小相等的初速度v0同时水平抛出,已知半圆轨道的半径与斜面竖直高度相等,斜面底边长是其竖直高度的2倍,若小球a能落到半圆轨道上,小球b能落到斜面上,则( )| A. | b球一定先落在斜面上 | |
| B. | a球可能垂直落在半圆轨道上 | |
| C. | a、b两球可能同时落在半圆轨道和斜面上 | |
| D. | a、b两球不可能同时落在半圆轨道和斜面上 |
11.某电场区域的电场线如图所示.一个电子以一定的初速度从A点运动到B点的过程,则( )


| A. | 电子所受的电场力增大,电子克服电场力做功 | |
| B. | 电子所受的电场力减小,电场力对电子做正功 | |
| C. | 电子的加速度增大,电势能减小 | |
| D. | 电子的加速度减小,电势能增大 |

 如图所示,半径为R的水平绝缘圆盘可绕竖直轴OO′转动,水平虚线AB、CD互相垂直,一电荷量为+q的可视为质点的小物块置于距转轴r处,空间有方向A指向B的匀强电场.当圆盘匀速转动时,小物块相对圆盘始终静止.小物块转动到位置Ⅰ(虚线AB上)时受到的摩擦力为零,转动到位置Ⅱ(虚线CD上)时受到的摩擦力为f.求:
如图所示,半径为R的水平绝缘圆盘可绕竖直轴OO′转动,水平虚线AB、CD互相垂直,一电荷量为+q的可视为质点的小物块置于距转轴r处,空间有方向A指向B的匀强电场.当圆盘匀速转动时,小物块相对圆盘始终静止.小物块转动到位置Ⅰ(虚线AB上)时受到的摩擦力为零,转动到位置Ⅱ(虚线CD上)时受到的摩擦力为f.求: