题目内容
【题目】从A点斜向上抛出一个小球,曲线ABCD是小球运动的一段轨迹.建立如图所示的正交坐标系xOy,x轴沿水平方向,轨迹上三个点的坐标分别为A(﹣L,0)、C(L,0),D(2L,3L),小球受到的空气阻力忽略不计,轨迹与y轴的交点B的坐标为( )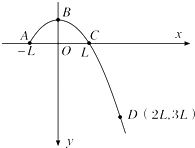
A.(0, ![]() )
)
B.(0,﹣L)
C.(0, ![]() )
)
D.(0,﹣2L)
【答案】B
【解析】解:由图像可知,小球的轨迹是二次函数,开口向下,且过A(﹣L,0)、C(L,0),
设轨迹方程为:y=﹣a(x﹣L)(x+L)
将D的坐标 x=2L,y=3L
代入上式得:a=﹣ ![]()
则 y= ![]() (x﹣L)(x+L)
(x﹣L)(x+L)
当x=0,得:y=﹣L,故B的坐标为(0,﹣L),故B正确,ACD错误.
故选:B.
由图知,小球的轨迹是二次函数,开口向下,且过A(﹣L,0)、C(L,0),可设轨迹方程为 y=﹣a(x﹣L)(x+L),将D点坐标代入求出a,再求解B的坐标.

【题目】下表是四种交通工具的速度改变情况,假设均为匀变速运动,下列说法正确的是( )
初始速度(m/s) | 经过时间(s) | 末速度(m/s) | |
甲 | 5 | 5 | 10 |
乙 | 0 | 10 | 10 |
丙 | 0 | 10 | 20 |
丁 | 0 | 20 | 30 |
A.甲的初速度最大,加速度最大
B.乙的速度变化最小
C.丙的速度变化最快
D.丁的末速度最大,加速度最大
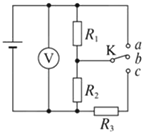
【题目】用下列器材测量电容器的电容:
一块多用电表,一台直流稳压电源,一个待测电容器(额定电压16V),定值电阻R1(阻值未知),定值电阻R2=150Ω,电流传感器、数据采集器和计算机,单刀双掷开关S,导线若干.
实验过程如下:
实验次数 | 实验步骤 |
第1次 | ①用多用电表的“×10”挡测量电阻R1 , 指针偏转如图甲所示. |
②将电阻R1等器材按照图乙正确连接电路,将开关S与1端连接,电源向电容器充电. | |
③将开关S掷向2端,测得电流随时间变化的i﹣t曲线如图丙中的实线a所示. | |
第2次 | ④用电阻R2替换R1 , 重复上述实验步骤②③,测得电流随时间变化的i﹣t曲线如图丁中的某条虚线所示. |
说明:两次实验中电源输出的直流电压恒定且相同. | |
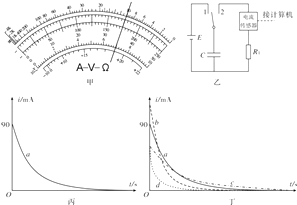
请完成下列问题:
(1)由图甲可知,电阻R1的测量值为Ω.
(2)第1次实验中,电阻R1两端的最大电压U=V.利用计算机软件测得i﹣t曲线和两坐标轴所围的面积为42.3mAS,已知电容器放电时其内阻可以忽略不计,则电容器的电容为C= .
(3)第2次实验中,电流随时间变化的i﹣t曲线应该是图丁中的虚线(选填“b”、“c”或“d”),判断依据是 .