题目内容
15.一质点在t=0时刻从坐标原点出发,沿x轴正方向做初速度为零,加速度大小为a1的匀加速直线运动,t=ls时到达x=5m的位置,速度大小为v1,此时加速度立即反向,加速度大小变为a2,t=3s时质点恰好回到原点,速度大小为v2,则( )| A. | a2=3a1 | |
| B. | v2=3v1 | |
| C. | 质点向x轴正方向运动的时间为2s | |
| D. | 质点向x轴正方向运动最远到x=9m的位置 |
分析 根据位移与平均速度的关系,以及速度公式,即可求出加速度的大小关系以及两个速度之间的关系.
解答 解:A、B、设第一段时间为t1,第二段时间为t2,1s末的速度为v1,最后的速度为v2,则:
$x=\frac{1}{2}{a}_{1}{t}_{1}^{2}$
代入数据得:a1=10m/s2
v1=a1t1,v2=a2t2-a1t1
由题意:$x=\frac{{v}_{1}}{2}•{t}_{1}=\frac{{v}_{2}-{v}_{1}}{2}•{t}_{2}$
联立得:${a}_{2}=12.5m/{s}^{2}$,v1=10m/s,v2=15m/s
即:${a}_{2}=\frac{5}{4}{a}_{1}$,${v}_{2}=\frac{3}{2}{v}_{1}$.故A错误,B错误;
C、质点向x轴正方向减速的时间为:${t}_{3}=\frac{{v}_{1}}{{a}_{2}}=\frac{10}{12.5}=0.8$s,所以质点向x轴正方向运动的时间为:t=t1+t3=1+0.8=1.8s.故C错误;
D、质点向x轴正方向运动最远的位置:${x}_{m}=\frac{{v}_{1}}{2}({t}_{1}+{t}_{3})=\frac{10}{2}×(1+0.8)=9$m.故D正确.
故选:D
点评 本题主要考查了匀变速直线运动位移时间公式及速度时间公式的直接应用,难度不大,属于中档题.

练习册系列答案
相关题目
5.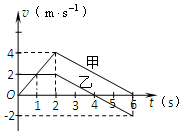 甲、乙两个物体从同一地点、沿同一直线同时做直线运动,其v-t图象如图所示,则下列说法错误的是( )
甲、乙两个物体从同一地点、沿同一直线同时做直线运动,其v-t图象如图所示,则下列说法错误的是( )
 甲、乙两个物体从同一地点、沿同一直线同时做直线运动,其v-t图象如图所示,则下列说法错误的是( )
甲、乙两个物体从同一地点、沿同一直线同时做直线运动,其v-t图象如图所示,则下列说法错误的是( )| A. | 2s时甲和乙相遇 | B. | 2~6s内甲相对乙做匀速直线运动 | ||
| C. | 2~6s内乙的加速度保持不变 | D. | 0~6s内甲乙相距最大距离为4m |
3.在人类对微观世界进行探索的过程中,科学实验起到了非常重要的作用.下列说法符合历史事实的是( )
| A. | 普朗克通过对光电效应实验的研究,确定了光的粒子性 | |
| B. | 汤姆孙通过阴极射线在电、磁场中偏转的实验,发现了原子内部存在电子 | |
| C. | 贝克勒尔通过对天然放射现象的研究,发现了原子中存在原子核 | |
| D. | 卢瑟福通过α粒子轰击氮核的实验,证实了在原子核内部存在中子 |
10.下列说法中正确的是( )
| A. | 奥斯特发现了电磁感应现象 | |
| B. | 牛顿通过理想斜面实验得出了维持运动不需要力的结论 | |
| C. | 玻尔的原子理论成功地解释了氢原子光谱现象,推动了量子理论的发展 | |
| D. | 光照在金属板上时,金属能否发生光电效应现象与入射光的强度有关 |
20.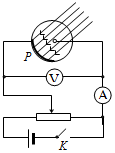 如图,当电键K断开时,用光子能量为3.8eV的一束光照射阴极P,发现电流表读数不为零.合上电键,调节滑线变阻器,发现当电压表读数小于1.6V时,电流表读数仍不为零;当电压表读数大于或等于1.6V时,电流表读数为零.由此可知阴极材料的逸出功为( )
如图,当电键K断开时,用光子能量为3.8eV的一束光照射阴极P,发现电流表读数不为零.合上电键,调节滑线变阻器,发现当电压表读数小于1.6V时,电流表读数仍不为零;当电压表读数大于或等于1.6V时,电流表读数为零.由此可知阴极材料的逸出功为( )
 如图,当电键K断开时,用光子能量为3.8eV的一束光照射阴极P,发现电流表读数不为零.合上电键,调节滑线变阻器,发现当电压表读数小于1.6V时,电流表读数仍不为零;当电压表读数大于或等于1.6V时,电流表读数为零.由此可知阴极材料的逸出功为( )
如图,当电键K断开时,用光子能量为3.8eV的一束光照射阴极P,发现电流表读数不为零.合上电键,调节滑线变阻器,发现当电压表读数小于1.6V时,电流表读数仍不为零;当电压表读数大于或等于1.6V时,电流表读数为零.由此可知阴极材料的逸出功为( )| A. | 5.4eV | B. | 1.6eV | C. | 3.8eV | D. | 2.2eV |
5.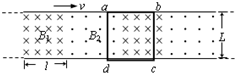 超导体磁悬浮列车是利用超导体的抗磁化作用使列车车体向上浮起,同时通过周期性地变换磁极方向而获得驱动力的新型交通工具.如图所示为磁悬浮列车的原理图,在水平面上,两根平行直导轨的间距为L,其间有竖直方向且等距离的匀强磁场B1和B2,磁场B1和B2导的截面均为有理想边界且边长为L的正方形,依次紧贴交替排列,导轨上放一个与导轨等宽的正方形金属框abcd.当匀强磁场B1和B2同时以某一速度v沿直轨道向右运动时,金属框也会沿直轨道运动.设金属框的电阻为R、运动中所受阻力恒为f;匀强磁场的磁感应强度为2B1=B2=B,则金属框的最大速度可表示为( )
超导体磁悬浮列车是利用超导体的抗磁化作用使列车车体向上浮起,同时通过周期性地变换磁极方向而获得驱动力的新型交通工具.如图所示为磁悬浮列车的原理图,在水平面上,两根平行直导轨的间距为L,其间有竖直方向且等距离的匀强磁场B1和B2,磁场B1和B2导的截面均为有理想边界且边长为L的正方形,依次紧贴交替排列,导轨上放一个与导轨等宽的正方形金属框abcd.当匀强磁场B1和B2同时以某一速度v沿直轨道向右运动时,金属框也会沿直轨道运动.设金属框的电阻为R、运动中所受阻力恒为f;匀强磁场的磁感应强度为2B1=B2=B,则金属框的最大速度可表示为( )
 超导体磁悬浮列车是利用超导体的抗磁化作用使列车车体向上浮起,同时通过周期性地变换磁极方向而获得驱动力的新型交通工具.如图所示为磁悬浮列车的原理图,在水平面上,两根平行直导轨的间距为L,其间有竖直方向且等距离的匀强磁场B1和B2,磁场B1和B2导的截面均为有理想边界且边长为L的正方形,依次紧贴交替排列,导轨上放一个与导轨等宽的正方形金属框abcd.当匀强磁场B1和B2同时以某一速度v沿直轨道向右运动时,金属框也会沿直轨道运动.设金属框的电阻为R、运动中所受阻力恒为f;匀强磁场的磁感应强度为2B1=B2=B,则金属框的最大速度可表示为( )
超导体磁悬浮列车是利用超导体的抗磁化作用使列车车体向上浮起,同时通过周期性地变换磁极方向而获得驱动力的新型交通工具.如图所示为磁悬浮列车的原理图,在水平面上,两根平行直导轨的间距为L,其间有竖直方向且等距离的匀强磁场B1和B2,磁场B1和B2导的截面均为有理想边界且边长为L的正方形,依次紧贴交替排列,导轨上放一个与导轨等宽的正方形金属框abcd.当匀强磁场B1和B2同时以某一速度v沿直轨道向右运动时,金属框也会沿直轨道运动.设金属框的电阻为R、运动中所受阻力恒为f;匀强磁场的磁感应强度为2B1=B2=B,则金属框的最大速度可表示为( )| A. | v | B. | $\frac{4fR}{9{B}^{2}{L}^{2}}$ | C. | v-$\frac{fR}{9{B}^{2}{L}^{2}}$ | D. | v-$\frac{4fR}{9{B}^{2}{L}^{2}}$ |
3.下列说法中正确的是( )
| A. | 动量不变的物体,动能一定不变 | B. | 动能不变的物体,动量一定不变 | ||
| C. | 动量变化的物体,动能一定变化 | D. | 动能变化的物体,动量可能变化 |
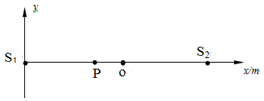 介质中x轴上有两个波源S1和S2,O是S1S2的中点,x轴上的P点与O点相距d=4m,如图所示.两波源同时开始沿y轴负方向振动,产生的简谐横波沿x轴相向传播,频率相等,波速相等,振幅均为A,波长满足2m<λ<8m.某一时刻质点P的位移为2A.
介质中x轴上有两个波源S1和S2,O是S1S2的中点,x轴上的P点与O点相距d=4m,如图所示.两波源同时开始沿y轴负方向振动,产生的简谐横波沿x轴相向传播,频率相等,波速相等,振幅均为A,波长满足2m<λ<8m.某一时刻质点P的位移为2A.