Question

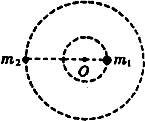
已知地球半径为R，月球半径为r，地球与月球中心之间的距离为s．月球公转周期为T₁，地球自转周期为T₂，地球公转周期为T₃，万有引力常量为G，由以上条件可知（　　）

A．地球的质量为M= 4π2s3 GT32

B．月球的质量为M= 4π2s3 GT12

C．地球的密度为ρ= 3π GT12

D．月球运动的加速度为a= 4π2s T12

Answer 1

A、研究月球绕地球圆周运动，利用万有引力提供向心力得：
G

Mm

r2

=mr

4π2

T12

解得：
M=

4π2s3

GT12

，故A错误
B、由于不知道月球的卫星的相关量，故不能求得月球质量，故B错误
C、研究在地球表面附近运行的人造卫星，利用万有引力提供向心力：
G

Mm

R2

=mR

4π2

T32

解得：M=

4π2R3

GT32

又：ρ=

M

V

=

4π2R3 GT32

4πR3 3

=

3π

GT32

，故C错误
D、月球向心加速度为：a=sω²=s×(

2π

T1

)2=

4π2s

T12

，故D正确
故选D