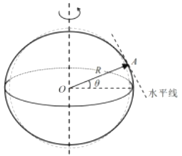
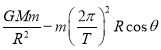题目内容
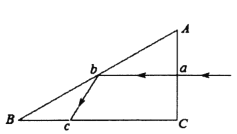
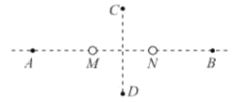
【题目】如图所示,在光滑水平面上,木块C置于足够长的木板A上的左端某处,A、C开始以v0=10m/s的初速度共同向右运动,与静止在地面上的B碰撞后,B立即获得vB=3m/s的速度。已知mA=1kg,mB=4kg,mC=2kg,A、C间接触面粗糙,试求:
(1)第一次碰撞瞬间A、B、C组成的系统损失的机械能;
(2)请分析说明,第一次碰撞后还能进行第二次碰撞吗?
![]()
【答案】(1)30J;(2)能
【解析】
(1)设向右为正方向,A、C开始以v0=10m/s的初速度共同向右运动,与B碰撞后B立即获得vB=3m/s的速度,由于碰撞时间极短,C的速度可认为还没有变化,A、B组成的系统动量守恒有
mAv0=mAvA+mBvB
解得碰后A的速度为:
vA=-2m/s
负号表示方向水平向左,大小为2m/s,第一次碰撞瞬间损失的机械能为:
![]()
(2)第一次碰撞后,A、C组成的系统动量守恒,设A、C稳定后的共同速度为vAC,则有
mAvA+mCv0=(mA+mC)vAC
可得:
vAC=6m/s
方向向右。因为vAC>vB,所以还能发生第二次碰撞。

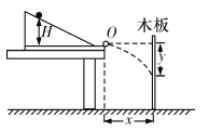
【题目】某同学利用如图所小的装置验证动能定理。将木板竖直放置在斜槽末端的前方某一固定位置,在木板上依次固定好白纸、复写纸。将小球从不同的标记点由静止释放,记录小球到达斜槽底端吋下落的高度H,并根据落点位置测量岀小球离开斜槽后的竖直位移y。改变小球在斜槽上的释放位置,进行多次测量,记录数据如下:
高度H(h为单位长度) | h | 2h | 3h | 4h | 5h | 6h | 7h | 8h | 9h |
竖直位移y/cm | 30.0 | 15.0 | 10.0 | 7.5 | 6.0 | 5.0 | 4.3 | 3.8 | 3.3 |
(1)在安装斜槽时,应注意____________;
(2)已知斜梄倾角为θ,小球与斜槽之间的动摩擦因数为μ,木板与斜槽末端的水平距离为x,小球在离开斜槽后的竖直位移为y,不计小球与水平槽之间的摩擦,小球从斜槽上滑下的过程中,若动能定理成立则应满足的关系式是_______。
(3)若想利用图象直观得到实验结论,最好应以H为横坐标,以_____为纵坐标,描点作图。