题目内容
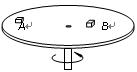
如下图所示，两个摩擦传动的轮子，A为主动轮，转动的角速度为ω，已知A、B轮的半径分别是R1和R2，C点离圆心捉为R2/2，则A、B、C三点的向心加速度之比为a1：a2：a3＝__________ C点处的向心加速度是______。
____ 2R2_：2 R1_： R1____ ____ R12ω2_/2 R2_______ m/s2
AB具有相同的线速度，根据
可知，向心加速度与半径成反比，即
a1：a2= R2：R1，BC具有相同的角速度，根据
可知，向心加速度与半径成正比，即a2：a3= R2：R2/2=2:1，所以a1：a2：a3＝2R2：2R1：R1，C点处的向心加速度是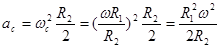
故答案为：2R2：2R1：R1，
可知，向心加速度与半径成反比，即a1：a2= R2：R1，BC具有相同的角速度，根据
可知，向心加速度与半径成正比，即a2：a3= R2：R2/2=2:1，所以a1：a2：a3＝2R2：2R1：R1，C点处的向心加速度是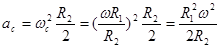故答案为：2R2：2R1：R1，
练习册系列答案
期末集结号系列答案
相关题目
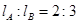，而转过的角度之比为
，则它们的运行周期之比为
到圆盘中心的距离. 
则A运动的周期____________（选填“大于”、“小于”或“等于”）B运动的周期；A的运动的线速度____________（选填“大于”、“小于”或“等于”）B运动的线速度. 