题目内容
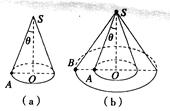
如图所示,甲球由轻绳系住,乙球由橡皮条系住,都从水平位置由静止开始
释放,当两球到达悬点正下方K点时,橡皮条长度恰好与绳长相等.则在K点
时两球的速度大小关系是( )

释放,当两球到达悬点正下方K点时,橡皮条长度恰好与绳长相等.则在K点
时两球的速度大小关系是( )

| A.v甲=v乙 | B.v甲>v乙 | C.v甲<v乙 | D.无法确定 |
B
分析:两小球初态时,处于同一高度,质量相等,重力势能相等,机械能相等,下摆过程中,甲球的重力势能全部转化为动能,而乙球的重力势能转化为动能和橡皮绳的弹性势能,这样,在最低点时,甲球的动能大,从而就能比较两球速度大小.
解答:解:取最低点所在水平面为参考平面.根据机械能守恒定律,得,对乙:mgl2=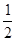 mv乙2+EP,EP为橡皮绳的弹性势能,对甲:mgl2=
mv乙2+EP,EP为橡皮绳的弹性势能,对甲:mgl2=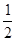 mv甲2,显然v甲>v乙故B正确,ACD错误.
mv甲2,显然v甲>v乙故B正确,ACD错误.
故选B
点评:本题既可定性分析,也可定量研究.关键抓住A、B机械能相等,A系统有三种形式的机械能,B只有两种形式的机械能,用机械能守恒的观点很快就能求解.
解答:解:取最低点所在水平面为参考平面.根据机械能守恒定律,得,对乙:mgl2=
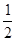 mv乙2+EP,EP为橡皮绳的弹性势能,对甲:mgl2=
mv乙2+EP,EP为橡皮绳的弹性势能,对甲:mgl2=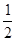 mv甲2,显然v甲>v乙故B正确,ACD错误.
mv甲2,显然v甲>v乙故B正确,ACD错误.故选B
点评:本题既可定性分析,也可定量研究.关键抓住A、B机械能相等,A系统有三种形式的机械能,B只有两种形式的机械能,用机械能守恒的观点很快就能求解.

练习册系列答案
相关题目
 杆从静止由水平转至竖直方向,A球在最低点时的速度为4 m/s.(g取10 m/s2)
杆从静止由水平转至竖直方向,A球在最低点时的速度为4 m/s.(g取10 m/s2)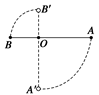
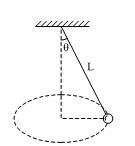
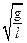 (l为摆长)
(l为摆长)