题目内容
19. 如图所示.两个劲度分别为K1、K2的弹簧,它们的上端分别固定在A、B点,两弹簧平行下垂,它们下端通过一个光滑的定滑轮连接在一起.当定滑轮的挂钩处挂上重为G的物体静止后滑轮轴下移$\frac{G({K}_{1}+{K}_{2})}{4{K}_{1}{K}_{2}}$.
如图所示.两个劲度分别为K1、K2的弹簧,它们的上端分别固定在A、B点,两弹簧平行下垂,它们下端通过一个光滑的定滑轮连接在一起.当定滑轮的挂钩处挂上重为G的物体静止后滑轮轴下移$\frac{G({K}_{1}+{K}_{2})}{4{K}_{1}{K}_{2}}$.
分析 对滑轮进行受力分析,应用平衡条件可求得弹簧的弹力,重物下降的距离就是两根弹簧伸长的量除以2
解答 解:对滑轮受力分析如图: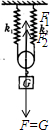
因为F1、F2是同一根绳上的力,故大小相等,即:F1=F2
由平衡条件得:F1+F2=G
解得:F1=$\frac{G}{2}$由胡克定律公式F=kx得:
弹簧1伸长量为:
x1=$\frac{\frac{G}{2}}{{K}_{1}}$=$\frac{G}{2{K}_{1}}$
弹簧2伸长量为:
x2=$\frac{\frac{G}{2}}{{K}_{2}}$=$\frac{G}{2{K}_{2}}$
弹簧共伸长:
x=x1+x2=$\frac{G}{2{K}_{1}}$+$\frac{G}{2{K}_{2}}$=$\frac{G({K}_{1}+{K}_{2})}{2{K}_{1}{K}_{2}}$
重物下降的距离为:d=$\frac{X}{2}$=$\frac{G({K}_{1}+{K}_{2})}{4{K}_{1}{K}_{2}}$
故答案为:$\frac{G({K}_{1}+{K}_{2})}{4{K}_{1}{K}_{2}}$
点评 本题为受力平衡的简单应用,受力分析后应用平衡条件,注意伸长量与下落的关系,求解即可

练习册系列答案
 习题精选系列答案
习题精选系列答案
相关题目
9.高血压是危害人体健康的一种常见病,现已查明,血管内径变细是其诱因之一.我们可以在简化假设下研究这个问题:设液体通过一根一定长度的管子时受到的阻力F与流速v成正比,即F=kv(为简便,设k与管子粗细无关);为维持液体匀速流过,在这段管子两端需有一定的压强差(以使压力差平衡阻力而使液体匀速流动).设血管截面积为S时两端压强差为p,若血管截面积减小10%时,为了维持在相同时间内流过同样多的液体,压强差必须变为( )
| A. | $\frac{100}{81}$p | B. | 100p | C. | $\frac{10}{9}$p | D. | 10 p |
7. 如图所示,有一固定的光滑斜面,其倾角θ=37°,顶端离地面的高度h=0.45m.现让一质量m=0.5kg的小物块从斜面顶端由静止滑下,当物块滑至斜面底端时重力的瞬时功率为(g取10m/s2)( )
如图所示,有一固定的光滑斜面,其倾角θ=37°,顶端离地面的高度h=0.45m.现让一质量m=0.5kg的小物块从斜面顶端由静止滑下,当物块滑至斜面底端时重力的瞬时功率为(g取10m/s2)( )
 如图所示,有一固定的光滑斜面,其倾角θ=37°,顶端离地面的高度h=0.45m.现让一质量m=0.5kg的小物块从斜面顶端由静止滑下,当物块滑至斜面底端时重力的瞬时功率为(g取10m/s2)( )
如图所示,有一固定的光滑斜面,其倾角θ=37°,顶端离地面的高度h=0.45m.现让一质量m=0.5kg的小物块从斜面顶端由静止滑下,当物块滑至斜面底端时重力的瞬时功率为(g取10m/s2)( )| A. | 4.5W | B. | 9W | C. | 12W | D. | 15W |
4.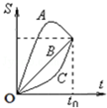 A、B、C三个物体从同一点出发,沿着一条直线运动的位移-时间(S-t)图象如图所示,下列说法中正确的是( )
A、B、C三个物体从同一点出发,沿着一条直线运动的位移-时间(S-t)图象如图所示,下列说法中正确的是( )
 A、B、C三个物体从同一点出发,沿着一条直线运动的位移-时间(S-t)图象如图所示,下列说法中正确的是( )
A、B、C三个物体从同一点出发,沿着一条直线运动的位移-时间(S-t)图象如图所示,下列说法中正确的是( )| A. | 三者者的位移不相等 | |
| B. | A物体做曲线运动 | |
| C. | 三个物体在0~t0时间内的平均速度vA>vC>vB | |
| D. | 三个物体在0~t0时间内的平均速度vA=vB=vC |
9.下列情境中,关于力的大小关系,说法正确的是( )
| A. | 跳高运动员起跳,地面对运动员的支持力大于运动员对地面的压力 | |
| B. | 钢丝绳吊起货物加速上升时,钢丝绳对货物的拉力大于货物对钢丝绳的拉力 | |
| C. | 鸡蛋撞击石头,鸡蛋破碎,石头对鸡蛋的作用力大于鸡蛋对石头的作用力 | |
| D. | 火箭加速上升时,火箭发动机的推力大于火箭的重力 |
 如图所示,物体沿着两个半径均为2.5m的半圆弧由A点运动到C点,A、B、C三点在同一直线上.在此过程中,物体位移的大小是4Rm,方向是由A指向C,物体通过的路程是2πRm.
如图所示,物体沿着两个半径均为2.5m的半圆弧由A点运动到C点,A、B、C三点在同一直线上.在此过程中,物体位移的大小是4Rm,方向是由A指向C,物体通过的路程是2πRm.
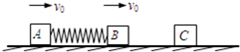 光滑水平面上,用弹簧相连接的质量均为2kg的A、B两物体,都以v0=6m/s的速度向右运动,弹簧处于原长;质量为4kg的物体C静止在前方,如图所示,B与C发生碰撞后(碰撞时间极短)粘合在一起运动,在以后的运动中,求:
光滑水平面上,用弹簧相连接的质量均为2kg的A、B两物体,都以v0=6m/s的速度向右运动,弹簧处于原长;质量为4kg的物体C静止在前方,如图所示,B与C发生碰撞后(碰撞时间极短)粘合在一起运动,在以后的运动中,求: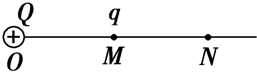 在真空中O点放一个电荷Q=+1.0×10-9C,直线MN通过O点,OM的距离r=30cm,M点放一个点电荷q=-1.0×10-10C,如图所示.
在真空中O点放一个电荷Q=+1.0×10-9C,直线MN通过O点,OM的距离r=30cm,M点放一个点电荷q=-1.0×10-10C,如图所示.