题目内容
9.高血压是危害人体健康的一种常见病,现已查明,血管内径变细是其诱因之一.我们可以在简化假设下研究这个问题:设液体通过一根一定长度的管子时受到的阻力F与流速v成正比,即F=kv(为简便,设k与管子粗细无关);为维持液体匀速流过,在这段管子两端需有一定的压强差(以使压力差平衡阻力而使液体匀速流动).设血管截面积为S时两端压强差为p,若血管截面积减小10%时,为了维持在相同时间内流过同样多的液体,压强差必须变为( )| A. | $\frac{100}{81}$p | B. | 100p | C. | $\frac{10}{9}$p | D. | 10 p |
分析 首先根据血液是匀速流动,说明受力平衡,即血压产生的压力等于阻力,可以列出在正常情况和血管变细两种情况下的等式;
然后根据两种情况下,血管在相同时间内流过的血液量不变,列出等式;
最后根据血管横截面积前后变化的定量关系,结合前面列出的等式,联立成方程组,就可求出答案.
解答 解:血管截面积为S时,因血液匀速流动,有 pS=kv,
血管截面积为S′=0.9S时,有p′S′=kv′,
由题:Sv=S′v′,
则得 $\frac{P′}{P}$=$\frac{{S}^{2}}{S{′}^{2}}$=$\frac{100}{81}$
故P'=$\frac{100}{81}$P;
故选:A.
点评 本题考查了平衡状态条件的应用和有关压强的计算,关键是找出血管变化前后的等量关系,再根据平衡条件进行分析才能准确求解.

练习册系列答案
相关题目
17.已知在弹性绳上传播的一列简谐横波在某一时刻的波形,则( )
| A. | 知道波的传播方向,就可确定此时绳上任一质点(速度不为零的质点)振动的速度方向 | |
| B. | 知道绳上一质点(速度不为零的质点)的振动速度方向,就可确定波的传播方向 | |
| C. | 波的传播周期等于绳上每一质点的振动周期 | |
| D. | 波在传播过程中,绳上的各质点将以波的传播速度沿着波形运动 |
4.下列说法中不正确的是( )
| A. | 一定质量的气体被压缩时,气体压强不一定增大 | |
| B. | 一定质量的气体温度不变压强增大时,其体积也增大 | |
| C. | 气体压强是由气体分子间的斥力产生的 | |
| D. | 在失重情况下,密闭容器内的气体对器壁没有压强 |
1.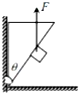 建筑装修中,工人用质量为m的磨石对倾角为θ的斜壁进行打磨,如图所示.当对磨石加竖直向上大小为F的推力时,磨石恰好沿斜壁向上匀速运动,已知磨石与斜壁之间的动摩擦因数为μ,则关于斜壁受到磨石的摩擦力的大小与方向,下列说法正确的是( )
建筑装修中,工人用质量为m的磨石对倾角为θ的斜壁进行打磨,如图所示.当对磨石加竖直向上大小为F的推力时,磨石恰好沿斜壁向上匀速运动,已知磨石与斜壁之间的动摩擦因数为μ,则关于斜壁受到磨石的摩擦力的大小与方向,下列说法正确的是( )
 建筑装修中,工人用质量为m的磨石对倾角为θ的斜壁进行打磨,如图所示.当对磨石加竖直向上大小为F的推力时,磨石恰好沿斜壁向上匀速运动,已知磨石与斜壁之间的动摩擦因数为μ,则关于斜壁受到磨石的摩擦力的大小与方向,下列说法正确的是( )
建筑装修中,工人用质量为m的磨石对倾角为θ的斜壁进行打磨,如图所示.当对磨石加竖直向上大小为F的推力时,磨石恰好沿斜壁向上匀速运动,已知磨石与斜壁之间的动摩擦因数为μ,则关于斜壁受到磨石的摩擦力的大小与方向,下列说法正确的是( )| A. | (F-mg)cosθ,沿斜壁向上 | B. | (F-mg)cosθ,沿斜壁向下 | ||
| C. | μ(F-mg)cosθ,沿斜壁向上 | D. | μ(F-mg)cosθ,沿斜壁向下 |
18.做直线运动的甲、乙两物体的位移-时间图象如图所示,则( )


| A. | 在0~10s这段时间内,物体间的距离逐渐变大 | |
| B. | 乙开始运动时,两物体相距20m | |
| C. | 在10s~25s这段时间内,甲的速度大于乙的速度 | |
| D. | 两物体在10s时相距最远,在25 s时相遇 |
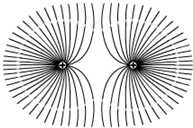 图展示了等量同种点电荷电场的电场线,由图可以看出,在两电荷的连线上,从左至右场强的大小变化情况是先变小后变大,在两电荷连线的中垂线上,从上(足够远)往下(足够远),场强的大小变化情况是先变大后变小再变大又变小,方向的变化情况是竖直向上变为竖直向下.
图展示了等量同种点电荷电场的电场线,由图可以看出,在两电荷的连线上,从左至右场强的大小变化情况是先变小后变大,在两电荷连线的中垂线上,从上(足够远)往下(足够远),场强的大小变化情况是先变大后变小再变大又变小,方向的变化情况是竖直向上变为竖直向下. 如图所示.两个劲度分别为K1、K2的弹簧,它们的上端分别固定在A、B点,两弹簧平行下垂,它们下端通过一个光滑的定滑轮连接在一起.当定滑轮的挂钩处挂上重为G的物体静止后滑轮轴下移$\frac{G({K}_{1}+{K}_{2})}{4{K}_{1}{K}_{2}}$.
如图所示.两个劲度分别为K1、K2的弹簧,它们的上端分别固定在A、B点,两弹簧平行下垂,它们下端通过一个光滑的定滑轮连接在一起.当定滑轮的挂钩处挂上重为G的物体静止后滑轮轴下移$\frac{G({K}_{1}+{K}_{2})}{4{K}_{1}{K}_{2}}$.