题目内容
1. A、D两点分别是斜面的顶端、底端,B、C是斜面上的两个点,LAB=LBC=LCD,E点在D点正上方并与A点等高.从E点以一定水平速度抛出质量相等的两个小球,球1落在B点,球2落在C点,球1和球2从抛出到落在斜面上的过程(不计空气阻力)中,( )
A、D两点分别是斜面的顶端、底端,B、C是斜面上的两个点,LAB=LBC=LCD,E点在D点正上方并与A点等高.从E点以一定水平速度抛出质量相等的两个小球,球1落在B点,球2落在C点,球1和球2从抛出到落在斜面上的过程(不计空气阻力)中,( )| A. | 两球运动的时间之比为1:$\sqrt{2}$ | B. | 两球抛出时初速度之比为2$\sqrt{2}$:1 | ||
| C. | 两球动能增加量之比为1:2 | D. | 两球重力做功之比为1:3 |
分析 平抛运动在水平方向上做匀速直线运动,在竖直方向上做自由落体运动,根据高度确定运动的时间,通过水平位移求出初速度之比.根据动能定理求出动能的增加量之比.
解答 解:A、因为AC=2AB,则AC的高度差是AB高度差的2倍,根据$h=\frac{1}{2}g{t}^{2}$得,t=$\sqrt{\frac{2h}{g}}$,解得运动的时间比为1:$\sqrt{2}$,故A正确.
B、AC在水平方向上的位移是AB在水平方向位移的2倍,结合x=v0t,解得初速度之比为$2\sqrt{2}:1$,故B正确.
C、根据动能定理得,mgh=△Ek,因为下降的高度之比为1;2,则重力做功为1:2,动能的增加量之比为 1:2,故C正确,D错误.
故选:ABC.
点评 解决本题的关键知道平抛运动在水平方向和竖直方向上的运动规律,结合运动学公式进行求解.

练习册系列答案
相关题目
12.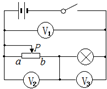 如图,电源电动势为3V,内阻不可忽略,滑动变阻器的滑片P从a滑向b的过程中,三只理想电压表的示数变化的绝对值分别为△U1、△U2、△U3,下列各值不可能出现的是( )
如图,电源电动势为3V,内阻不可忽略,滑动变阻器的滑片P从a滑向b的过程中,三只理想电压表的示数变化的绝对值分别为△U1、△U2、△U3,下列各值不可能出现的是( )
 如图,电源电动势为3V,内阻不可忽略,滑动变阻器的滑片P从a滑向b的过程中,三只理想电压表的示数变化的绝对值分别为△U1、△U2、△U3,下列各值不可能出现的是( )
如图,电源电动势为3V,内阻不可忽略,滑动变阻器的滑片P从a滑向b的过程中,三只理想电压表的示数变化的绝对值分别为△U1、△U2、△U3,下列各值不可能出现的是( )| A. | △U1=3V、△U2=2V、△U3=1V | B. | △U1=1V、△U2=3V、△U3=2V | ||
| C. | △U1=0.5V、△U2=1V、△U3=1.5V | D. | △U1=0.2V、△U2=1V、△U3=0.8V |
9.关于声波的描述,下述正确的是( )
| A. | 同一列声波在各种介质中的波长是相同的 | |
| B. | 声波的频率越高,它在空气中传播的速度越快 | |
| C. | 人能辨别不同乐器同时发出的声音,说明声波不会发生干涉 | |
| D. | “隔墙有耳”说明声波可以绕过障碍物传播,即它可以发生衍射 |
16.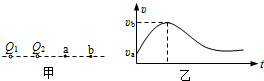 如图甲,Q1、Q2为两个固定着的点电荷,a、b是它们连线的延长线上的两点.现有一点电荷,只在电场力作用下,以一定的初速度沿直线从a点开始经b点向远处运动,其υ-t图象如图乙,电子经过a、b两点的速度分别为υa、υb,则( )
如图甲,Q1、Q2为两个固定着的点电荷,a、b是它们连线的延长线上的两点.现有一点电荷,只在电场力作用下,以一定的初速度沿直线从a点开始经b点向远处运动,其υ-t图象如图乙,电子经过a、b两点的速度分别为υa、υb,则( )
 如图甲,Q1、Q2为两个固定着的点电荷,a、b是它们连线的延长线上的两点.现有一点电荷,只在电场力作用下,以一定的初速度沿直线从a点开始经b点向远处运动,其υ-t图象如图乙,电子经过a、b两点的速度分别为υa、υb,则( )
如图甲,Q1、Q2为两个固定着的点电荷,a、b是它们连线的延长线上的两点.现有一点电荷,只在电场力作用下,以一定的初速度沿直线从a点开始经b点向远处运动,其υ-t图象如图乙,电子经过a、b两点的速度分别为υa、υb,则( )| A. | Q1一定带正电 | B. | Q1的电量一定小于Q2的电量 | ||
| C. | b点的电场强度一定为0 | D. | 电子的电势能先增大后减小 |
10.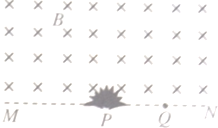 如图所示,在直线MN上方存在着垂直于纸面向里的匀强磁场,放置直线MN上P点的粒子源(粒子均带负电),可以向磁场区域纸面内的各个方向发射出比荷k和速率v均相同的粒子,PQ间距离等于粒子的轨道半径R,则过Q点的离子的运动时间为( )
如图所示,在直线MN上方存在着垂直于纸面向里的匀强磁场,放置直线MN上P点的粒子源(粒子均带负电),可以向磁场区域纸面内的各个方向发射出比荷k和速率v均相同的粒子,PQ间距离等于粒子的轨道半径R,则过Q点的离子的运动时间为( )
 如图所示,在直线MN上方存在着垂直于纸面向里的匀强磁场,放置直线MN上P点的粒子源(粒子均带负电),可以向磁场区域纸面内的各个方向发射出比荷k和速率v均相同的粒子,PQ间距离等于粒子的轨道半径R,则过Q点的离子的运动时间为( )
如图所示,在直线MN上方存在着垂直于纸面向里的匀强磁场,放置直线MN上P点的粒子源(粒子均带负电),可以向磁场区域纸面内的各个方向发射出比荷k和速率v均相同的粒子,PQ间距离等于粒子的轨道半径R,则过Q点的离子的运动时间为( )| A. | $\frac{2πR}{v}$ | B. | $\frac{πR}{3v}$ | C. | $\frac{5πR}{3v}$ | D. | $\frac{πR}{v}$ |
 如图,绷紧的传送带与水平面的夹角θ=30°,传送带在电动机的带动下,始终保持v0=2m/s的速率运行.现把一质量m=30kg的工件(可看做质点)轻轻放在皮带的底端,经时间t=1.9s,工件被传送到h=1.5m的高处,取g=10m/s2.求:
如图,绷紧的传送带与水平面的夹角θ=30°,传送带在电动机的带动下,始终保持v0=2m/s的速率运行.现把一质量m=30kg的工件(可看做质点)轻轻放在皮带的底端,经时间t=1.9s,工件被传送到h=1.5m的高处,取g=10m/s2.求: 匀强磁场中有一半径为0.2m的圆形闭合线圈,线圈平面与磁场垂直.已知线圈共50匝,其阻值为2Ω.匀强磁场磁感应强度B在0~1s内从零均匀变化到0.2T,在1~5s内从0.2T均匀变化到-0.2T.则0.5s 时该线圈内感应电动势的大小E=1.256V;在1~5s内通过线圈的电荷量q=1.256C.
匀强磁场中有一半径为0.2m的圆形闭合线圈,线圈平面与磁场垂直.已知线圈共50匝,其阻值为2Ω.匀强磁场磁感应强度B在0~1s内从零均匀变化到0.2T,在1~5s内从0.2T均匀变化到-0.2T.则0.5s 时该线圈内感应电动势的大小E=1.256V;在1~5s内通过线圈的电荷量q=1.256C. 由粗细两段组成的管道固定在竖直平面内,粗、细管横截面积分别为2S、S.细管底部由光滑“工”字型轻活塞封闭.初始时细管内水银柱和被封闭气体位置尺寸如图所示,水银上表面恰位于粗细管连接处.外界大气压p0=76cmHg柱:
由粗细两段组成的管道固定在竖直平面内,粗、细管横截面积分别为2S、S.细管底部由光滑“工”字型轻活塞封闭.初始时细管内水银柱和被封闭气体位置尺寸如图所示,水银上表面恰位于粗细管连接处.外界大气压p0=76cmHg柱: 如图,某同学在一次实验测试中,利用弹簧枪将质量为m的钢珠以某一初速度从A点水平射出,发现钢珠能够恰好从弯曲圆管BCD的B点无撞击地进入圆弧,最终从圆管的最高点D射出后落到斜面上的E点,已知两圆弧的半径为均R,且A与D在同一水平线上,图中角θ=60°,斜面上O′到E点距离也为R,求
如图,某同学在一次实验测试中,利用弹簧枪将质量为m的钢珠以某一初速度从A点水平射出,发现钢珠能够恰好从弯曲圆管BCD的B点无撞击地进入圆弧,最终从圆管的最高点D射出后落到斜面上的E点,已知两圆弧的半径为均R,且A与D在同一水平线上,图中角θ=60°,斜面上O′到E点距离也为R,求