题目内容
17.一质量为2.5kg的物体受到劲度系数为k=250N/m的弹簧的作用而做简谐运动,设开始计时时系统所具有的动能Ek=0.2J,势能EP=0.6J.(1)振动的振幅为多少?
(2)振动的周期T,角速度ω,频率f为多少?
(3)T=0时,位移的大小应为多少?
(4)如果已知初相位φ0在第一象限,求出φ0.
(5)写出振动方程.
分析 (1)据弹簧振子的能量守恒求解.(2)据弹簧振子的周期公式求解.(3)据弹簧的能量公式求解位移.(4)据初相位在第一象限求出初相位.(5)据振动方程表达式写出即可.
解答 解析(1)由于弹簧振子振动过程能量守恒,所以E=$\frac{1}{2}$KA2=Ek+EP=0.2J+0.6J=0.8J.
代入数据解得:A=0.08m
(2)据弹簧振子的振动周期得:T=2π$\sqrt{\frac{m}{k}}$=$\sqrt{\frac{2.5}{250}}$s≈0.63s,
f=$\frac{1}{T}$=1.6Hz,
ω=2πf=10rad/s
(3)据弹簧的势能公式得:x=$\sqrt{\frac{2{E}_{p}}{k}}$=$\sqrt{\frac{1.2}{250}}$m≈0.069m
(4)由于初相位φ0在第一象限x=0.069m=0.08cosφ0
解得:φ0≈300=$\frac{π}{6}$
(5)振动方程为x=0.08cos(10t+$\frac{π}{6}$)m
答:1)振动的振幅为0.08m.
(2)振动的周期0.63s,角速度10rad/s,频率f为1.6Hz.
(3)T=0时,位移的大小应为0.069m.
(4)如果已知初相位φ0在第一象限,初相位为$\frac{π}{6}$.
(5)写出振动方程x=0.08cos(10t+$\frac{π}{6}$)m.
点评 本题看似简单,但是综合的知识点较多,注意弹簧的弹性势能、振子的周期公式、简谐运动的表达式和各物理量间的关系,基础题.

 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案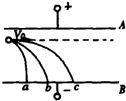 如图所示,有三个质量相等分别带正电、负电和不带电的小球,从平行板电场中的左侧以相同的初速垂直于电场方向进入电场,它们分别落到A、B、C三点,则可以断定( )
如图所示,有三个质量相等分别带正电、负电和不带电的小球,从平行板电场中的左侧以相同的初速垂直于电场方向进入电场,它们分别落到A、B、C三点,则可以断定( )| A. | 落到a点的小球带正电,落到C点的小球带负电 | |
| B. | 三小球在电场中运动时间相等 | |
| C. | 三小球到达负极板的动能关系是EKA>EKB>EKC | |
| D. | 三小球在电场中运动的加速度是aA>aB>aC |
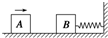 如图所示,木块A和B质量均为2kg,置于光滑水平面上,B与一轻质弹簧一端相连,弹簧另一端固定在竖直挡板上,当A以4m/s速度向B撞击时,由于有橡皮泥而使A、B粘在一起运动,那么弹簧被压缩到最短时,具有的弹性势能大小为( )
如图所示,木块A和B质量均为2kg,置于光滑水平面上,B与一轻质弹簧一端相连,弹簧另一端固定在竖直挡板上,当A以4m/s速度向B撞击时,由于有橡皮泥而使A、B粘在一起运动,那么弹簧被压缩到最短时,具有的弹性势能大小为( )| A. | 4J | B. | 8J | C. | 16J | D. | 32J |
| A. | 速度越小 | B. | 周期越大 | C. | 向心加速度越大 | D. | 角速度越大 |
 如图所示,有一束平行于等边三棱镜截面ABC的单色光从空气射向E点,并偏折到F点.已知入射方向与边AB的夹角为θ=30°,E、F分别为边AB、BC的中点,则( )
如图所示,有一束平行于等边三棱镜截面ABC的单色光从空气射向E点,并偏折到F点.已知入射方向与边AB的夹角为θ=30°,E、F分别为边AB、BC的中点,则( )| A. | 光从空气进入棱镜,波长变大 | |
| B. | 光从空气进入棱镜,光速变大 | |
| C. | 该棱镜的折射率为$\sqrt{3}$ | |
| D. | 从F点出射的光束与入射到E点的光束平行 |
| A. | 物体的速率可能不变 | |
| B. | 物体一定做匀变速曲线运动,且速率一定增大 | |
| C. | 物体可能做匀速圆周运动 | |
| D. | 物体受到的合力与速度的夹角一定越来越小 |
 如图所示,一根细线下端拴着一个金属小球P,细线的上端固定在一个金属块Q上,Q放在带小孔(小孔光滑)的水平面上,小球P在某一水平面内做匀速圆周运动.现使P在更高一些的水平面内做匀速圆周运动,两次金属块Q都静止在桌面的同一位置,则后一种情况与原来的情况相比( )
如图所示,一根细线下端拴着一个金属小球P,细线的上端固定在一个金属块Q上,Q放在带小孔(小孔光滑)的水平面上,小球P在某一水平面内做匀速圆周运动.现使P在更高一些的水平面内做匀速圆周运动,两次金属块Q都静止在桌面的同一位置,则后一种情况与原来的情况相比( )| A. | 小球P运动的角速度变小 | B. | 小球P运动的向心加速度变大 | ||
| C. | 小球Q受到的静摩擦力变大 | D. | 细线所受拉力变小 |
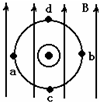 如图所示,在竖直向上的匀强磁场中,水平放置着一根长直流导线,电流方向指向读者,a、b、c、d是以直导线为圆心的同一圆周上的四点,在这四点中( )
如图所示,在竖直向上的匀强磁场中,水平放置着一根长直流导线,电流方向指向读者,a、b、c、d是以直导线为圆心的同一圆周上的四点,在这四点中( )| A. | a、b两点磁感应强度大小相等 | B. | a点磁感应强度最大 | ||
| C. | b点磁感应强度最大 | D. | c、d两点磁感应强度大小相等 |
| A. | 布朗运动就是分子的运动 | |
| B. | 布朗运动是组成固体微粒的分子无规则运动的反映 | |
| C. | 布朗运动是液体分子无规则运动的反映 | |
| D. | 液体的温度越高,悬浮微粒越小,布朗运动越显著 |