题目内容
8.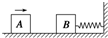 如图所示,木块A和B质量均为2kg,置于光滑水平面上,B与一轻质弹簧一端相连,弹簧另一端固定在竖直挡板上,当A以4m/s速度向B撞击时,由于有橡皮泥而使A、B粘在一起运动,那么弹簧被压缩到最短时,具有的弹性势能大小为( )
如图所示,木块A和B质量均为2kg,置于光滑水平面上,B与一轻质弹簧一端相连,弹簧另一端固定在竖直挡板上,当A以4m/s速度向B撞击时,由于有橡皮泥而使A、B粘在一起运动,那么弹簧被压缩到最短时,具有的弹性势能大小为( )| A. | 4J | B. | 8J | C. | 16J | D. | 32J |
分析 木块A和B碰撞过程,两木块组成的系统动量守恒,根据动量守恒定律求出碰后的共同速度,木块压缩弹簧后在弹簧弹力作用下做减速运动,当系统动能为零时,弹簧被压缩到最短,弹簧的弹性势能最大,根据能量守恒定律求出弹簧具有的最大弹性势能.
解答 解:对于木块A和B碰撞过程,两木块组成的系统动量守恒,取向右为正方向,由动量守恒定律得:
mvA=2mv;
得 v=0.5vA=2m/s
弹簧被压缩到最短时,具有的弹性势能大小为 Ep=$\frac{1}{2}•2m{v}^{2}$=2×22J=8J
故选:B.
点评 本题综合考查了动量守恒定律和能量守恒定律,关键要知道木块碰撞过程系统的动量守恒,此过程弹簧未参与,系统的动能全部转化为弹性势能时,弹性势能最大.

练习册系列答案
相关题目
18.已知地球质量为M,半径为R,自转周期为T,地球同步卫星质量为m,引力常量为G,有关同步卫星下列说法正确的是( )
| A. | 卫星的轨道半径为$\root{3}{{\frac{{GM{T^2}}}{{4{π^2}}}}}$ | |
| B. | 卫星的运行速度小于第一宇宙速度 | |
| C. | 卫星运行时受到的向心力大小为G$\frac{Mm}{R^2}$ | |
| D. | 卫星运行的向心加速度小于地球表面的重力加速度 |
16. 如图所示的电路可将声音信号转化为电信号,该电路中b是固定不动的金属板,a是能在声波驱动下沿水平方向振动的镀有金属层的振动膜,a、b构成了一个电容器,且通过导线与恒定电源两极相接,若声源S发出声波,则a振动过程中( )
如图所示的电路可将声音信号转化为电信号,该电路中b是固定不动的金属板,a是能在声波驱动下沿水平方向振动的镀有金属层的振动膜,a、b构成了一个电容器,且通过导线与恒定电源两极相接,若声源S发出声波,则a振动过程中( )
 如图所示的电路可将声音信号转化为电信号,该电路中b是固定不动的金属板,a是能在声波驱动下沿水平方向振动的镀有金属层的振动膜,a、b构成了一个电容器,且通过导线与恒定电源两极相接,若声源S发出声波,则a振动过程中( )
如图所示的电路可将声音信号转化为电信号,该电路中b是固定不动的金属板,a是能在声波驱动下沿水平方向振动的镀有金属层的振动膜,a、b构成了一个电容器,且通过导线与恒定电源两极相接,若声源S发出声波,则a振动过程中( )| A. | a、b板之间的电场强度不变 | |
| B. | a、b板上所带的电荷量不变 | |
| C. | 电路中始终有方向不变的电流 | |
| D. | 当a板向右位移最大时,电容器电容最大 |
20.如图所示,物体静止在固定鞋面上,物体受到的力有( )
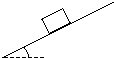

| A. | 重力、支持力和摩擦力 | B. | 重力、摩擦力和下滑力 | ||
| C. | 重力、摩擦力和平衡力 | D. | 重力、弹力和平衡力 |
4. 竖直虚线MN两侧存在垂直纸面向里的匀强磁场,两磁场的磁感应强度相等,上边界在同一水平线上,区域Ⅰ磁场高3L,区域Ⅱ磁场高为L.两个完全相同的正方形线圈位于竖直平面内,边长为L,质量为m,电阻为R,底边始终与磁场上边界平行,现让线圈1从磁场上方高4L处,线圈2从磁场上方一定高度处均由静止释放,结果发现,线圈1刚进入磁场时的速度与刚到这磁场下边界时速度相等,线圈2刚好能匀速通过且穿过磁场时的速度与线圈1刚好完全进入磁场时的速度相等,则下列说法正正确的是( )
竖直虚线MN两侧存在垂直纸面向里的匀强磁场,两磁场的磁感应强度相等,上边界在同一水平线上,区域Ⅰ磁场高3L,区域Ⅱ磁场高为L.两个完全相同的正方形线圈位于竖直平面内,边长为L,质量为m,电阻为R,底边始终与磁场上边界平行,现让线圈1从磁场上方高4L处,线圈2从磁场上方一定高度处均由静止释放,结果发现,线圈1刚进入磁场时的速度与刚到这磁场下边界时速度相等,线圈2刚好能匀速通过且穿过磁场时的速度与线圈1刚好完全进入磁场时的速度相等,则下列说法正正确的是( )
 竖直虚线MN两侧存在垂直纸面向里的匀强磁场,两磁场的磁感应强度相等,上边界在同一水平线上,区域Ⅰ磁场高3L,区域Ⅱ磁场高为L.两个完全相同的正方形线圈位于竖直平面内,边长为L,质量为m,电阻为R,底边始终与磁场上边界平行,现让线圈1从磁场上方高4L处,线圈2从磁场上方一定高度处均由静止释放,结果发现,线圈1刚进入磁场时的速度与刚到这磁场下边界时速度相等,线圈2刚好能匀速通过且穿过磁场时的速度与线圈1刚好完全进入磁场时的速度相等,则下列说法正正确的是( )
竖直虚线MN两侧存在垂直纸面向里的匀强磁场,两磁场的磁感应强度相等,上边界在同一水平线上,区域Ⅰ磁场高3L,区域Ⅱ磁场高为L.两个完全相同的正方形线圈位于竖直平面内,边长为L,质量为m,电阻为R,底边始终与磁场上边界平行,现让线圈1从磁场上方高4L处,线圈2从磁场上方一定高度处均由静止释放,结果发现,线圈1刚进入磁场时的速度与刚到这磁场下边界时速度相等,线圈2刚好能匀速通过且穿过磁场时的速度与线圈1刚好完全进入磁场时的速度相等,则下列说法正正确的是( )| A. | 两个线圈在进入磁场过程中产生逆时针方向的感应电流 | |
| B. | 线圈2开始下落时距磁场上边界高L | |
| C. | 线圈1在进入磁场过程中产生热量是2mgL | |
| D. | 匀强磁场的磁感应强度大约为$\frac{\sqrt{mgR}}{L}$•$\root{4}{4gL}$ |
 如图所示,一直角三棱镜截面ABC,∠ABC=30°,∠ACB=90°斜边长为L,其折射率为n=$\sqrt{3}$,一束平行光从斜边距A点$\frac{L}{3}$处的O点平行于BC边射入该棱镜.(光在真空中的速度为c,不考虑光的反射.)
如图所示,一直角三棱镜截面ABC,∠ABC=30°,∠ACB=90°斜边长为L,其折射率为n=$\sqrt{3}$,一束平行光从斜边距A点$\frac{L}{3}$处的O点平行于BC边射入该棱镜.(光在真空中的速度为c,不考虑光的反射.)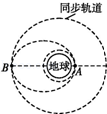 发射地球同步卫星时,先将卫星发射到距地面高度为h1的圆轨道上,在卫星经过A点时点火实施变轨进入椭圆轨道,最后在椭圆轨道的远地点B点再次点火将卫星送入同步轨道,如图所示.已知同步卫星的运动周期为T,地球的半径为R,地球表面重力加速度为g,忽略地球自转的影响.求:
发射地球同步卫星时,先将卫星发射到距地面高度为h1的圆轨道上,在卫星经过A点时点火实施变轨进入椭圆轨道,最后在椭圆轨道的远地点B点再次点火将卫星送入同步轨道,如图所示.已知同步卫星的运动周期为T,地球的半径为R,地球表面重力加速度为g,忽略地球自转的影响.求: 在“探究弹力和弹簧伸长量的关系”实验中.
在“探究弹力和弹簧伸长量的关系”实验中.