题目内容
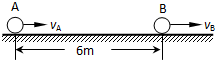
如图所示,A、B两物体相距6m,A以vA=4m/s的速度向右做匀速直线运动;图示时刻B的速度vB=6m/s,在摩擦力作用下做匀减速运动,加速度大小为a=2m/s2,求:
(1)从图示时刻开始,经过多少时间B与A的速度相同?此时它们相距多远?
(2)从图示时刻开始,经过多少时间A追上B?
(1)从图示时刻开始,经过多少时间B与A的速度相同?此时它们相距多远?
(2)从图示时刻开始,经过多少时间A追上B?

(1)根据VB-a?t=VA得
t=
=
=1s
此时B的位移SB=
?t=
×1=5m
则两者相距的距离SAB=S0-VA?t+SB=6-4×1+5=7m.
(2)先判断A追上B是在B停下前还是停下后,设B经t′停下,
有t′=
=
=3s
此时B的位移SB′=
?t′=
×3=9m
因△S=S0+SB′-VA?t'=6+9-4×3=3m>0,所以B停下时,A还未追上.
此后B停止不动,A匀速运动,有△S=VA?t″,
得t″=
=
=0.75s,
t总=t′+t″=3+0.75=3.75s.
答:(1)经过1sA、B的速度相同,此时它们相距7m.
(2)经过3.75s后追上.
t=
| VB-VA |
| a |
| 6-4 |
| 2 |
此时B的位移SB=
| VA+VB |
| 2 |
| 4+6 |
| 2 |
则两者相距的距离SAB=S0-VA?t+SB=6-4×1+5=7m.
(2)先判断A追上B是在B停下前还是停下后,设B经t′停下,
有t′=
| VB-0 |
| a |
| 6 |
| 2 |
此时B的位移SB′=
| VB+0 |
| 2 |
| 6 |
| 2 |
因△S=S0+SB′-VA?t'=6+9-4×3=3m>0,所以B停下时,A还未追上.
此后B停止不动,A匀速运动,有△S=VA?t″,
得t″=
| △S |
| VA |
| 3 |
| 4 |
t总=t′+t″=3+0.75=3.75s.
答:(1)经过1sA、B的速度相同,此时它们相距7m.
(2)经过3.75s后追上.

练习册系列答案
 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案
相关题目
