题目内容
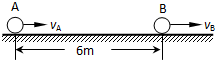
甲、乙两车从同一地点同向行驶,但是甲车做匀速直线运动,其速度为v=20米/秒,乙车在甲车行驶至距离出发地200米处时开始以初速度为零、加速度为a=2米/秒2追甲.求:
(1)乙车追上甲车前两车间的最大距离.
(2)乙车追上甲车时,乙车运动了多长时间(可保留根号).
(1)乙车追上甲车前两车间的最大距离.
(2)乙车追上甲车时,乙车运动了多长时间(可保留根号).
(1)两车相遇前距离最大时两车速度必然相等,则运动时间t为:
t=
=
s=10s
∴△x=x0+x甲-x乙=x0+vt-
at2=200+20×10-
×2×102m=300m
(2)设经过时间t′后两车相遇,则有:
at′2=vt′+x0
×2×t′2=20t′+200
解得:t′=10(1+
)s
答:(1)乙车追上甲车前两车间的最大距离为300m.
(2)乙车追上甲车时,乙车运动的时间为10(1+
)s.
t=
| v |
| a |
| 20 |
| 2 |
∴△x=x0+x甲-x乙=x0+vt-
| 1 |
| 2 |
| 1 |
| 2 |
(2)设经过时间t′后两车相遇,则有:
| 1 |
| 2 |
| 1 |
| 2 |
解得:t′=10(1+
| 3 |
答:(1)乙车追上甲车前两车间的最大距离为300m.
(2)乙车追上甲车时,乙车运动的时间为10(1+
| 3 |

练习册系列答案
相关题目