题目内容
火星和木星沿各自的椭圆轨道绕太阳运行,根据开普勒行星运动定律可知:
| A.太阳位于木星运行轨道的中心 |
| B.火星和木星绕太阳运行速度的大小始终相等 |
| C.火星与木星公转周期之比的平方等于它们轨道半长轴之比的立方 |
| D.相同时间内,火星与太阳连线扫过的面积等于木星与太阳连线扫过的面积 |
C
根据开普勒第一定律可判断太阳位于椭圆的焦点上;开普勒第二定律描述行星的运动速度,在相等时间扫过的面积相等是针对同一行星的;开普勒第三定律指出所有行星绕同一恒星公转周期的平方与其轨道半长轴的立方的比值为一常数。
根据开普勒行星运动第一定律知:太阳不在中心,而在椭圆轨道的一个焦点上,故A错误;火星和木星绕太阳运行的轨道不同,则速度大小不可能始终相等,故B错误;开普勒第二定律知:在相等时间内,太阳和运动中的行星的连线所扫过的面积都是相等的,这里的行星是针对某一个,不是两个,故D项错误;根据第三定律知:所有行星公转周期的平方与它们轨道半长轴的立方之比等于一定值,即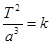 ,由于都绕太阳运动,故常数k相等,即
,由于都绕太阳运动,故常数k相等,即 ,所以有
,所以有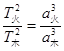 ,故C项正确。本题答案为C。
,故C项正确。本题答案为C。
【考点定位】本题考查开普勒行星运动三定律的理解。难度:中等偏低。
根据开普勒行星运动第一定律知:太阳不在中心,而在椭圆轨道的一个焦点上,故A错误;火星和木星绕太阳运行的轨道不同,则速度大小不可能始终相等,故B错误;开普勒第二定律知:在相等时间内,太阳和运动中的行星的连线所扫过的面积都是相等的,这里的行星是针对某一个,不是两个,故D项错误;根据第三定律知:所有行星公转周期的平方与它们轨道半长轴的立方之比等于一定值,即
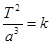 ,由于都绕太阳运动,故常数k相等,即
,由于都绕太阳运动,故常数k相等,即 ,所以有
,所以有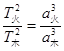 ,故C项正确。本题答案为C。
,故C项正确。本题答案为C。【考点定位】本题考查开普勒行星运动三定律的理解。难度:中等偏低。

练习册系列答案
 全优点练单元计划系列答案
全优点练单元计划系列答案
相关题目

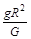
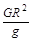
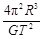
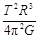
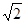 —1)R
—1)R