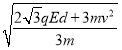题目内容
【题目】如图所示,长为L的细绳上端系一质量不计的环,环套在光滑的水平杆上,在细绳的下端吊一个质量为m的铁球(可视为质点),球离地的高度h=L。现让环与球一起以v=![]() 的速度向右运动,在A处环被挡住而立即停止,已知A离右墙的水平距离也为L,当地的重力加速度为g,不计空气阻力。求:
的速度向右运动,在A处环被挡住而立即停止,已知A离右墙的水平距离也为L,当地的重力加速度为g,不计空气阻力。求:
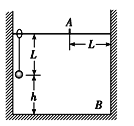
(1)在环被挡住而立即停止时绳对小球的拉力大小;
(2)若在环被挡住后,细绳突然断裂,则在以后的运动过程中,球的第一次碰撞点离墙角B点的距离是多少?
【答案】(1) ![]() (2)
(2) ![]()
【解析】
(1)环在A处被挡住立即停止,小球以速度v绕A点做圆周运动,据牛顿第二定律和圆周运动的向心力公式有:![]()
解得:绳对小球的拉力大小![]()
(2)在环被挡住后,细绳突然断裂,此后小球做平抛运动.
假设小球直接落在地面上,则:
竖直方向:![]()
水平方向:![]()
联立解得:小球的水平位移![]()
所以小球与右墙碰撞后再落在地上
设小球平抛运动到右墙的时间为![]() ,则:
,则:
![]()
小球在![]() 内下降的高度
内下降的高度![]()
球的第一次碰撞点离墙角B点的距离![]()

练习册系列答案
 高效智能课时作业系列答案
高效智能课时作业系列答案 捷径训练检测卷系列答案
捷径训练检测卷系列答案 小夫子全能检测系列答案
小夫子全能检测系列答案
相关题目