Question

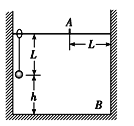
【题目】如图所示，足够长的“L”形长木板B置于粗糙的水平地面上，其上静止着可视为质点的滑块A，滑块距长木板右側壁距离为l＝6．5m，已知滑块与长木板、长木板与地面间的动摩擦因数均为0．1，A、B质量分别为mA＝2kg、mB＝1kg．现给A向右的瞬时冲量I＝14Ns，假设A与B右侧壁的碰撞为弹性碰撞，最大静摩擦力等于滑动摩擦力，g取

10m／s2．求

（1）A、B碰后瞬间，两者的速度大小

（2）最终滑块A距长木板B右側壁的距离．

Answer 1

【答案】(1)，；(2)d=3m

【解析】

小滑块A沿斜面下滑的过程，运用动能定理列式，可求得当A刚滑上B的上表面时的速度v0的大小。滑块A滑上木板B后，分析B的运动情况，根据牛顿第二定律可求得两者的加速度。最终A刚好未从木板B上滑下，A滑到B的右端，两者速度相等，

(1)施加冲量瞬间，对A由动量定理知：

在A向右运动过程，，B保持静止，对A有：

解得：

A、B弹性碰撞有：

解得：；

(2)碰后，A做加速运动，B做减速运动，由牛顿第二定律有：

对A：

对B：

设经时间A、B同速：

，得：

此时

假设A、B此后一起减速运动，

此进，假设成立，最终一起静止，

作出全过程图象，

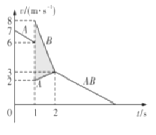
由图象可知图中阴影面积为滑块A距长木板B右侧的距离，即。