题目内容
(20分)如图所示,水平虚线x下方区域分布着方向水平、垂直纸面向里、磁感应强度为B的匀强磁场,整个空间存在匀强电场(图中未画出)。质量为m,电荷量为+q的小球P静止于虚线x上方A点,在某一瞬间受到方向竖直向下、大小为I的冲量作用而做匀速直线运动。在A点右下方的磁场中有定点O,长为l的绝缘轻绳一端固定于O点,另一端连接不带电的质量同为m的小球Q,自然下垂。保持轻绳伸直,向右拉起Q,直到绳与竖直方向有一小于50的夹角,在P开始运动的同时自由释放Q,Q到达O点正下方W点时速率为v0。P、Q两小球在W点发生正碰,碰后电场、磁场消失,两小球粘在一起运动。P、Q两小球均视为质点,P小球的电荷量保持不变,绳不可伸长,不计空气阻力,重力加速度为g。
(1)求匀强电场场强E的大小和P进入磁场时的速率v;
(2)若绳能承受的最大拉力为F,要使绳不断,F至少为多大?
(3)若P与Q在W点相向(速度方向相反)碰撞时,求A点距虚线X的距离s。
(1)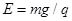
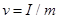 (2)
(2)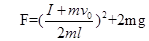 (3)
(3) 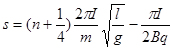 (n为大于
(n为大于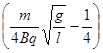 的整数)
的整数)
解析试题分析:(1)设小球P所受电场力为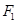 ,则
,则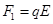 ①
①
在整个空间重力和电场力平衡,有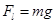 ②
②
联立相关方程得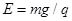 ③
③
设小球P受到冲量后获得速度为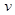 ,由动量定理得
,由动量定理得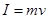 ④
④
得: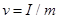 ⑤
⑤
(2)设P、Q同向相碰后在W点的速度最大,最大速度为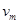 ,由动量守恒定律得:
,由动量守恒定律得: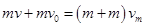 ⑥
⑥
此刻速度最大轻绳的张力也为最大,由牛顿运动定律得: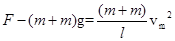 ⑦
⑦
联立相关方程,得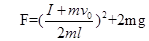 ⑧
⑧
(3)设P在X上方做匀速直线运动的时间为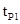 ,则
,则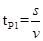 ⑨
⑨
设P在X下方做匀速圆周运动的时间为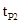 ,则:
,则: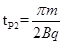 ⑩
⑩
设小球Q从开始运动到与P球相向碰撞的运动时间为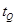 ,由单摆周期性有:
,由单摆周期性有: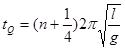 ?
?
由题意,有: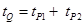 ?
?
联立相关方程,得: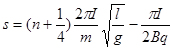 (n为大于
(n为大于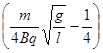 的整数) ?
的整数) ?
考点:带电粒子在复合场中的运动 动量守恒定律 单摆

 名校课堂系列答案
名校课堂系列答案

 kg的小车静止在光滑的水平面上,小车上有一质量
kg的小车静止在光滑的水平面上,小车上有一质量 kg的光滑小球,将一轻质弹簧压缩并锁定,此时弹簧的弹性势能为
kg的光滑小球,将一轻质弹簧压缩并锁定,此时弹簧的弹性势能为 J,小球脱离弹簧后与小车右壁的油灰阻挡层碰撞并被粘住,L=1.2m。求:
J,小球脱离弹簧后与小车右壁的油灰阻挡层碰撞并被粘住,L=1.2m。求: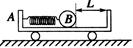
 沿BC的连线方向朝B运动,与B相碰并粘合在一起,以后细线突然断开,弹簧伸展,从而使C与A,B分离,已知C离开弹簧后的速度恰为
沿BC的连线方向朝B运动,与B相碰并粘合在一起,以后细线突然断开,弹簧伸展,从而使C与A,B分离,已知C离开弹簧后的速度恰为


 的大小;
的大小;