题目内容

如图所示，竖直平面内一光滑水平轨道左边与墙壁对接，右边与一足够高的1／4光滑圆弧轨道相连，木块A、B静置于光滑水平轨道上，A、B质量分别为1.5kg和0.5kg。现让A以6m/s的速度水平向左运动，之后与墙壁碰撞，碰撞时间为0.3s，碰后速度大小变为4m/s。当A与B碰撞后会立即粘在一起运动，已知g=10m/s2 求：

①A与墙壁碰撞过程中，墙壁对小球平均作用力F；
②A、B滑上圆弧轨道的最大高度。

 ①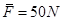方向水平向②h=0.45m

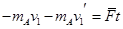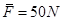解析试题分析：①设水平向右为正方向，当A与墙壁碰撞时根据动能定理有：；解得方向水平向左
②当A与B碰撞时，设碰撞后两物体的速度为v，根据动量守恒定律有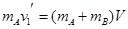
A B在光滑圆形轨道上升时，机械能守恒，由机械能守恒定律得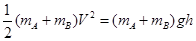
，解得h=0.45m
考点：动量守恒定律的应用

练习册系列答案
相关题目

在光滑的水平面上有两个在同一直线上相向运动的小球，其中甲球的质量m1=2kg，乙球的质量m2=1kg，规定向右为正方向，碰撞前后乙球的速度随时间变化情况如图所示。已知两球发生正碰后，甲球静止不动，碰撞时间极短，则碰前甲球速度的大小和方向分别为（  ）

A．0.5m／s，向右  B．0.5m／s，向左 
C．1.5m／s，向左 D．1.5m／s，向右 

如图所示，将两条完全相同的磁铁（磁性极强）分别固定在质量相等的小车上，水平面光滑，开始时甲车速度大小为3m/s，方向水平向右，乙车速度大小为2m/s，方向水平向左，两车在同一直线上，当乙车的速度为零时，甲车速度为________m/s，方向________。

(1)如图给出氢原子最低的4个能级，一群氢原子处于量子数最高为4的能级，这些氢原子跃迁所辐射的光子的频率最多有________种，其中最小频率为________，要使基态氢原子电离，应用波长为________的光照射氢原子(已知h＝6.63×10－34 J·s)．

(2)光滑水平地面上停放着甲、乙两辆平板车，一根轻绳跨过乙车的定滑轮(不计定滑轮的质量和摩擦)，绳的一端与甲车相连，另一端被甲车上的人拉在手中，已知每辆车和人的质量均为30 kg，两车间的距离足够远．现在人用力拉绳，两车开始相向运动，人与甲车保持相对静止，当乙车的速度为0.5 m/s时，停止拉绳．

①人在拉绳过程做了多少功？
②若人停止拉绳后，至少应以多大速度立即从甲车跳到乙车才能使两车不发生碰撞？

(10分) 质量分别为m1和m2的甲、乙两小球碰撞后在同一直线上运动，它们碰撞前、后的图象如图 (a)和图 (b)所示。求：

（1）碰撞前，甲、乙两小球的速度分别是多大；
（2）碰撞后，甲、乙两小球的速度分别是多大；
（3）求甲、乙两小球的质量之比m1：m2。

室内装修污染四大有害气体是苯系物、甲醛、氨气和氡。氡存在于建筑水泥、矿渣砖、装饰石材及土壤中。氡看不到，嗅不到，但它进入人的呼吸系统能诱发肺癌，是除吸烟外导致肺癌的重大因素。静止的氡核放出一个粒子x后变成钋核，钋核的动能为0.33MeV，若衰变放出的能量全部变成钋核和粒子x的动能。则：
①写出上述衰变的核反应方程；
②求粒子x的动能。（保留两位有效数字）

如图所示，质量mB＝2kg的平板车B上表面水平，开始时静止在光滑水平面上，在平板车左端静止着一块质量mA＝2kg的物块A，一颗质量m0＝0.01kg的子弹以v0＝600m/s的水平初速度瞬间射穿A后，速度变为v＝200m/s。已知A与B之间的动摩擦因数不为零，且A与B最终达到相对静止，则整个过程中Ａ、B组成的系统因摩擦产生的热量为多少？

（20分）如图所示，水平虚线x下方区域分布着方向水平、垂直纸面向里、磁感应强度为B的匀强磁场，整个空间存在匀强电场（图中未画出）。质量为m，电荷量为+q的小球P静止于虚线x上方A点，在某一瞬间受到方向竖直向下、大小为I的冲量作用而做匀速直线运动。在A点右下方的磁场中有定点O，长为l的绝缘轻绳一端固定于O点，另一端连接不带电的质量同为m的小球Q，自然下垂。保持轻绳伸直，向右拉起Q，直到绳与竖直方向有一小于50的夹角，在P开始运动的同时自由释放Q，Q到达O点正下方W点时速率为v0。P、Q两小球在W点发生正碰，碰后电场、磁场消失，两小球粘在一起运动。P、Q两小球均视为质点，P小球的电荷量保持不变，绳不可伸长，不计空气阻力，重力加速度为g。

（1）求匀强电场场强E的大小和P进入磁场时的速率v；
（2）若绳能承受的最大拉力为F，要使绳不断，F至少为多大？
（3）若P与Q在W点相向（速度方向相反）碰撞时，求A点距虚线X的距离s。

(9分)质量为M＝2 kg的小平板车C静止在光滑水平面上，车的一端静止着质量为mA＝2 kg的物体A(可视为质点)，如图所示，一颗质量为mB＝20 g的子弹以600 m/s的水平速度射穿A后，速度变为100 m/s，最后物体A静止在车上，求：

（1）平板车最后的速度是多少？
（2）整个系统损失的机械能是多少

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网