题目内容
(4分)如图所示，质量分别为m1和m2的两个小球在光滑的水平面上分别以速度v1、v2同向运动并发生对心碰撞，碰撞后m2被右侧墙壁原速率弹回，又与m1相碰，碰后两球都静止，求：两球第一次碰撞后m1的速度。
v′1＝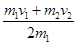
解析试题分析：以水平向右方向为正方向，第一次碰撞后瞬间，小球m1和m2的速度分别为v′1和v′2，整个碰撞过程两球系统的动量守恒，有：m1v1＋m2v2＝m1v′1＋m2v′2，m1v′1－m2v′2＝0，联立以上两式解得第一次碰撞后m1的速度为：v′1＝。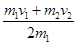
考点：本题主要考查了动量守恒定律的应用问题，属于中档偏低题。
练习册系列答案
相关题目
v0的速率反弹，试通过计算判断发生的是不是弹性碰撞．
）是一种人造同位素，可通过下列反应合成：
）轰击铀（
）生成镎（
）和两个相同的粒子x ，核反应方程是
；
。则x 粒子的符号为 ；Y 粒子的符号为 。
关于碰撞的特点，下列说法正确的是（ ）
| A．碰撞的过程时间极短 |
| B．碰撞时，质量大的物体对质量小的物体作用力大 |
| C．碰撞时，质量大的物体对质量小的物体作用力和质量小的物体对质量大的物体的作用力相等 |
| D．质量小的物体对质量大的物体作用力大 |
关于弹簧振子的振动，下述说法中正确的有
| A．周期与振幅有关，振幅越小，周期越小 |
| B．在任意的T/2内，速度变化总相同 |
| C．在任意的T/2内，弹力做功为零 |
| D．在最大位移处，因为速度为零，所以处于平衡状态 |