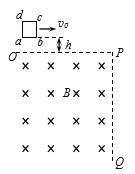
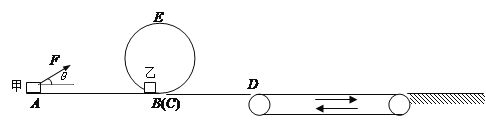
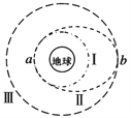
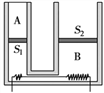
题目内容
【题目】如图所示，半径为R的透明半球体，在半球体右侧平行底面放置一个光屏。现在有一束平行单色光垂直半球底面射向透明半球体，经半球体折射后在光屏上形成光斑，将光屏由半球体顶部向右平移至距顶部
处时，光斑逐渐减小为半径为
的圆。已知光在真空中的传播速度为c，求：
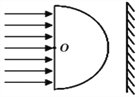
①透明半球体对该单色光的折射率；
②从底面圆心Ｏ处射入的单色光在透明半球体内传播的时间。
【答案】(1)
(2)
【解析】试题分析：①根据题意作出光路图，根据几何关系求出临界角的正弦值，根据
求出折射率；②根据
求出光在透明半球体内传播速度，根据
求出该光在透明半球体内传播时间。
①单色乐在透明半球体内以临界角C入射球面的光路图，如图所示
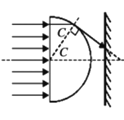
由几何知识得：
解得：
则透明半球体对该单色光的折射率为
②光在透明半球体内传播速度为
则该光在透明半球体内传播时间为
练习册系列答案
金钥匙试卷系列答案
相关题目
