题目内容
20.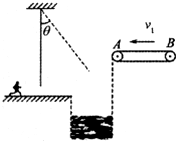 如图所示,在游乐节目中,选手需要借助悬挂在高处的绳飞越到对面的高台上.一质量m=60kg的选手脚穿轮滑鞋以v0=7m/s的水平速度抓住竖直的绳开始摆动,选手可看作质点,绳子的悬挂点到选手的距离l=6m.当绳摆到与竖直方向夹角θ=37°时,选手放开绳子,不考虑空气阻力和绳的质量.取重力加速度g=l0m/s2,sin37°=0.6.cos 37°=0.8.求:
如图所示,在游乐节目中,选手需要借助悬挂在高处的绳飞越到对面的高台上.一质量m=60kg的选手脚穿轮滑鞋以v0=7m/s的水平速度抓住竖直的绳开始摆动,选手可看作质点,绳子的悬挂点到选手的距离l=6m.当绳摆到与竖直方向夹角θ=37°时,选手放开绳子,不考虑空气阻力和绳的质量.取重力加速度g=l0m/s2,sin37°=0.6.cos 37°=0.8.求:(1)选手放开绳子时的速度大小;
(2)选手放开绳子后继续运动,到最高点时,刚好可以站到水平传送带A点,传送带始终以v=3m/s的速度匀速向左运动,传送带的另一端B点就是终点,且sAB=3.75m.若选手在传送带上自由滑行,受到的摩擦阻力为自重的0.2倍.
①通过计算说明该选手是否能顺利冲过终点B.
②求出选手在传送带上滑行过程中因摩擦而产生的热量Q.
分析 (1)选手拉着绳子在摆动的过程中机械能守恒,根据机械能守恒定律求出选手放开绳子时的速度大小.
(2)根据平行四边形定则求出选手放开绳子时水平方向和竖直方向上的分速度,当选手到达最高点时,竖直方向上的分速度为零,选手在传送带上的初速度等于水平分速度,结合牛顿第二定律和运动学公式求出选手在传送带上滑行的位移,从而判断能否顺利冲过终点.求出选手相对于传送带的路程,根据Q=f△s求出摩擦而产生的热量.
解答 解:(1)对选手从抓住绳子到放开绳子的整个过程中,由机械能守恒定律得
$\frac{1}{2}$mv02=mgL(1-cos37°)+$\frac{1}{2}$mv2;
解得:选手放开绳子时的速度 v=5m/s.
(2)①选手在放开绳子时,水平速度为vx,竖直速度为vy,则
vx=vcos37°=4m/s.
选手在最高点站到传送带上A点有4m/s向右的速度,在传送带上做匀减速直线运动.
选手的加速度大小 a=$\frac{kmg}{m}$=2m/s2.
以地面为参考系,由
-vx2=-2ax,
解得 x=4m>3.75m,所以选手可以顺利冲过终点B.
②设选手从A到B的时间为t,则
sAB=vxt-$\frac{1}{2}$at2;
解得t1=1.5s,t2=2.5s(舍去)
在这段时间内传送带通过的位移为:x1=v1t=4.5m.
摩擦力做功为:Wf=Q=kmg(sAB+x1)=990J.
答:
(1)选手放开绳子时的速度大小为5m/s.
(2)①选手可以顺利冲过终点B.②选手在传送带上滑行过程中因摩擦而产生的热量Q为990J.
点评 解决本题的关键要理清选手的运动情况,根据机械能守恒定律、牛顿第二定律和运动学公式以及功能关系进行解答.

练习册系列答案
相关题目
11.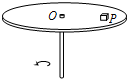 如图所示,在一个水平圆盘上有一个木块P随圆盘一起匀速转动.若圆盘的转速逐渐减慢,则下面说法中正确的是( )
如图所示,在一个水平圆盘上有一个木块P随圆盘一起匀速转动.若圆盘的转速逐渐减慢,则下面说法中正确的是( )
 如图所示,在一个水平圆盘上有一个木块P随圆盘一起匀速转动.若圆盘的转速逐渐减慢,则下面说法中正确的是( )
如图所示,在一个水平圆盘上有一个木块P随圆盘一起匀速转动.若圆盘的转速逐渐减慢,则下面说法中正确的是( )| A. | P受到的静摩擦力的方向仍然指向圆心 | |
| B. | P受到的静摩擦力不可能为零 | |
| C. | P受到的静摩擦力的方向跟P与O的连线的夹角大于90° | |
| D. | P受到的静摩擦力的方向跟P与O的连线的夹角等于90° |
15.如图所示,“神舟10号”宇宙飞船绕地球沿椭圆形轨道运动,它在A、B、C三点运动速率( )
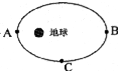

| A. | 一样大 | B. | 经过A点时最大 | C. | 经过B点时最大 | D. | 经过C点时最大 |
5. 如图所示,a、b两条曲线是汽车a、b在同一条平直公路上行驶时的速度-时间图象.已知在t1时刻两车相遇,下列说法正确的是( )
如图所示,a、b两条曲线是汽车a、b在同一条平直公路上行驶时的速度-时间图象.已知在t1时刻两车相遇,下列说法正确的是( )
 如图所示,a、b两条曲线是汽车a、b在同一条平直公路上行驶时的速度-时间图象.已知在t1时刻两车相遇,下列说法正确的是( )
如图所示,a、b两条曲线是汽车a、b在同一条平直公路上行驶时的速度-时间图象.已知在t1时刻两车相遇,下列说法正确的是( )| A. | t2时刻两车再次相遇 | |
| B. | t2时刻b车在前,a车在后 | |
| C. | a车加速度先增大后减小,b车加速度先减小后增大 | |
| D. | 从t1 到t2时间内两车加速度都是先减小后增大 |
 如图所示,重力为G的光滑球系在一细绳上,用细绳通过一小滑轮向水平方向缓慢拉小球,使它沿光滑墙上升.当细绳在小滑轮和小球间的长度刚好等于球的半径时,细绳的拉力和墙对球的支持力各是多大?在小球上升的过程中,细绳的拉力和墙对球的支持力如何变化?
如图所示,重力为G的光滑球系在一细绳上,用细绳通过一小滑轮向水平方向缓慢拉小球,使它沿光滑墙上升.当细绳在小滑轮和小球间的长度刚好等于球的半径时,细绳的拉力和墙对球的支持力各是多大?在小球上升的过程中,细绳的拉力和墙对球的支持力如何变化? 如图所示,我国“辽宁”号航空母舰上装有帮助飞机起飞的弹射系统.已知“歼-10”型战斗机在跑道上加速度时产生的最大加速度为5m/s2,起飞的最小速度是60m/s,弹射系统能够使飞机所具有的最大速度为20m/s,问:
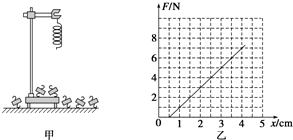
如图所示,我国“辽宁”号航空母舰上装有帮助飞机起飞的弹射系统.已知“歼-10”型战斗机在跑道上加速度时产生的最大加速度为5m/s2,起飞的最小速度是60m/s,弹射系统能够使飞机所具有的最大速度为20m/s,问: 某同学为了测定气垫导轨上滑块的加速度,他在滑块上安装了宽度d=2cm的遮光板,如图所示.然后利用气垫导轨和数字毫秒计记录了遮光板通过第一个光电门所用的时间为△t1=0.1s,通过第二个光电门的时间为△t2=0.05s,遮光板从开始遮住第一个光电门到开始遮住第二个光电门的时间为t=2s,则滑块的加速度大小为0.1m/s2,请提出减少实验误差的两点建议:减小遮光板的宽度,增大两光电门之间的距离.
某同学为了测定气垫导轨上滑块的加速度,他在滑块上安装了宽度d=2cm的遮光板,如图所示.然后利用气垫导轨和数字毫秒计记录了遮光板通过第一个光电门所用的时间为△t1=0.1s,通过第二个光电门的时间为△t2=0.05s,遮光板从开始遮住第一个光电门到开始遮住第二个光电门的时间为t=2s,则滑块的加速度大小为0.1m/s2,请提出减少实验误差的两点建议:减小遮光板的宽度,增大两光电门之间的距离.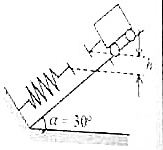 如图所示,自动卸料车连同料重为G1,它从静止开始沿着与水平面成30°的斜面滑下,滑到底端时与处于自然状态的轻弹簧相碰,当弹簧压缩到最大时,卸料车就自动翻斗卸料,此时料车下降高度为h,然后,依靠被压缩弹簧的弹性力作用又沿斜面回到原有高度,设空车重量为G2,另外假定摩擦阻力为车重的0.2倍,求G1与G2的比值.
如图所示,自动卸料车连同料重为G1,它从静止开始沿着与水平面成30°的斜面滑下,滑到底端时与处于自然状态的轻弹簧相碰,当弹簧压缩到最大时,卸料车就自动翻斗卸料,此时料车下降高度为h,然后,依靠被压缩弹簧的弹性力作用又沿斜面回到原有高度,设空车重量为G2,另外假定摩擦阻力为车重的0.2倍,求G1与G2的比值.