题目内容
10. 如图所示,重力为G的光滑球系在一细绳上,用细绳通过一小滑轮向水平方向缓慢拉小球,使它沿光滑墙上升.当细绳在小滑轮和小球间的长度刚好等于球的半径时,细绳的拉力和墙对球的支持力各是多大?在小球上升的过程中,细绳的拉力和墙对球的支持力如何变化?
如图所示,重力为G的光滑球系在一细绳上,用细绳通过一小滑轮向水平方向缓慢拉小球,使它沿光滑墙上升.当细绳在小滑轮和小球间的长度刚好等于球的半径时,细绳的拉力和墙对球的支持力各是多大?在小球上升的过程中,细绳的拉力和墙对球的支持力如何变化?
分析 以小球为研究对象,分析受力,由平衡条件得出绳对球的拉力与墙壁对球的支持力大小,根据两个力的表达式分析其变化.
解答 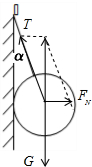 解:由几何知识可得:绳子与墙壁间的夹角为:α=30°
解:由几何知识可得:绳子与墙壁间的夹角为:α=30°
以小球为研究对象,分析受力如图.根据平衡条件,有:
T=$\frac{G}{cosα}$=$\frac{G}{cos30°}$=$\frac{2\sqrt{3}}{3}$G
FN=Gtanα=Gtan30°=$\frac{3}{4}$G
在小球上升的过程中,α增大,cosα减小,tanα增大,由上式可得 T增大,FN增大.
答:细绳的拉力和墙对球的支持力各是$\frac{2\sqrt{3}}{3}$G和$\frac{3}{4}$G,在小球上升的过程中,细绳的拉力和墙对球的支持力都增大.
点评 本题是简单的三力平衡问题,关键是受力分析后根据平衡条件并结合图示法分析.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
20.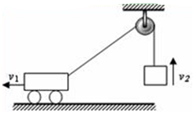 如图所示,在水平地面上做匀速直线运动的小车,通过定滑轮用绳子吊起一个物体,若小车和被吊的物体在同一时刻速度分别为v1和v2,绳子对物体的拉力为T,物体所受重力为G,则下面说法正确的是( )
如图所示,在水平地面上做匀速直线运动的小车,通过定滑轮用绳子吊起一个物体,若小车和被吊的物体在同一时刻速度分别为v1和v2,绳子对物体的拉力为T,物体所受重力为G,则下面说法正确的是( )
 如图所示,在水平地面上做匀速直线运动的小车,通过定滑轮用绳子吊起一个物体,若小车和被吊的物体在同一时刻速度分别为v1和v2,绳子对物体的拉力为T,物体所受重力为G,则下面说法正确的是( )
如图所示,在水平地面上做匀速直线运动的小车,通过定滑轮用绳子吊起一个物体,若小车和被吊的物体在同一时刻速度分别为v1和v2,绳子对物体的拉力为T,物体所受重力为G,则下面说法正确的是( )| A. | 物体做匀速运动,且v1=v2 | B. | 物体做加速运动,且v2<v1 | ||
| C. | 小车做匀速运动,且T>G | D. | 小车做匀速运动,且T=G |
1.关于速度、速度的变化量和加速度的关系,下列说法正确的是( )
| A. | 物体的加速度增大时,速度也增大 | |
| B. | 物体的速度变化越快,加速度越大 | |
| C. | 物体的速度变化量越大,则加速度越大 | |
| D. | 物体的速度和加速度同向时,速度一定增大 |
18. 利用如图所示装置可测磁感应强度,矩形线圈宽为L,共N匝,磁场垂直于纸面,当线圈中通以方向如图所示的电流I时,天平达到平衡状态.当电流改为反方向时(大小不变),右边再加质量为m的砝码后,天平重新平衡,由此可知( )
利用如图所示装置可测磁感应强度,矩形线圈宽为L,共N匝,磁场垂直于纸面,当线圈中通以方向如图所示的电流I时,天平达到平衡状态.当电流改为反方向时(大小不变),右边再加质量为m的砝码后,天平重新平衡,由此可知( )
 利用如图所示装置可测磁感应强度,矩形线圈宽为L,共N匝,磁场垂直于纸面,当线圈中通以方向如图所示的电流I时,天平达到平衡状态.当电流改为反方向时(大小不变),右边再加质量为m的砝码后,天平重新平衡,由此可知( )
利用如图所示装置可测磁感应强度,矩形线圈宽为L,共N匝,磁场垂直于纸面,当线圈中通以方向如图所示的电流I时,天平达到平衡状态.当电流改为反方向时(大小不变),右边再加质量为m的砝码后,天平重新平衡,由此可知( )| A. | 磁感应强度的方向垂直纸面向里,大小为$\frac{{(m}_{1}+{m}_{2})g}{NIL}$ | |
| B. | 磁感应强度的方向垂直纸面向里,大小为$\frac{mg}{2NIL}$ | |
| C. | 磁感应强度的方向垂直纸面向外,大小为$\frac{({m}_{1}-{m}_{2})g}{NIL}$ | |
| D. | 磁感应强度的方向垂直纸面向外,大小为$\frac{mg}{2NIL}$ |
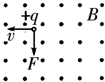
5.如图所示,AB为一条电场线,关于A、B两点处的物理量,下述说法中正确的是( )


| A. | A点的场强一定大于B点的场强 | |
| B. | A点的电势一定高于B点的电势 | |
| C. | A、B两点间的电势差一定等于E•d(E为A点的场强) | |
| D. | 电子在A点的电势能一定大于在B点的电势能 |
15. 如图所示的杂技演员在表演水流星的节目时,手持两端系有盛水的杯子的绳子中点在竖直面内做圆周运动,若两只杯子内盛水的质量相等,当一只杯子在最高点时水恰好不洒出来,这时另一只杯子中的水对杯底的压力大小是水的重力的( )
如图所示的杂技演员在表演水流星的节目时,手持两端系有盛水的杯子的绳子中点在竖直面内做圆周运动,若两只杯子内盛水的质量相等,当一只杯子在最高点时水恰好不洒出来,这时另一只杯子中的水对杯底的压力大小是水的重力的( )
 如图所示的杂技演员在表演水流星的节目时,手持两端系有盛水的杯子的绳子中点在竖直面内做圆周运动,若两只杯子内盛水的质量相等,当一只杯子在最高点时水恰好不洒出来,这时另一只杯子中的水对杯底的压力大小是水的重力的( )
如图所示的杂技演员在表演水流星的节目时,手持两端系有盛水的杯子的绳子中点在竖直面内做圆周运动,若两只杯子内盛水的质量相等,当一只杯子在最高点时水恰好不洒出来,这时另一只杯子中的水对杯底的压力大小是水的重力的( )| A. | 2倍 | B. | 4倍 | C. | 5倍 | D. | 6倍 |
19.下列关于电流的说法中,正确的是( )
| A. | 电荷移动的方向就是电流的方向 | |
| B. | 国际单位制中,电流的单位是安培,简称安 | |
| C. | 电流既有大小又有方向,所以电流是矢量 | |
| D. | 由I=$\frac{Q}{t}$可知,时间越长,电流越小 |


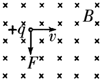
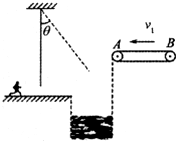 如图所示,在游乐节目中,选手需要借助悬挂在高处的绳飞越到对面的高台上.一质量m=60kg的选手脚穿轮滑鞋以v0=7m/s的水平速度抓住竖直的绳开始摆动,选手可看作质点,绳子的悬挂点到选手的距离l=6m.当绳摆到与竖直方向夹角θ=37°时,选手放开绳子,不考虑空气阻力和绳的质量.取重力加速度g=l0m/s2,sin37°=0.6.cos 37°=0.8.求:
如图所示,在游乐节目中,选手需要借助悬挂在高处的绳飞越到对面的高台上.一质量m=60kg的选手脚穿轮滑鞋以v0=7m/s的水平速度抓住竖直的绳开始摆动,选手可看作质点,绳子的悬挂点到选手的距离l=6m.当绳摆到与竖直方向夹角θ=37°时,选手放开绳子,不考虑空气阻力和绳的质量.取重力加速度g=l0m/s2,sin37°=0.6.cos 37°=0.8.求: