��Ŀ����
9��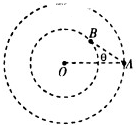 ��ͼ��ʾ����������A��B��ͬһƽ�����Ƶ���O��ͬ�������Բ���˶���A��B������A��O����ļнǦ���ʱ�䷢���仯�������ֵΪ��0������B��Բ���˶�������ΪT�����B��A���������Цȳ������ֵ��ʼ��ʱ����BԶ��A�����Цȳ������ֵ������ʱ���õ�ʱ��Ϊ��������
��ͼ��ʾ����������A��B��ͬһƽ�����Ƶ���O��ͬ�������Բ���˶���A��B������A��O����ļнǦ���ʱ�䷢���仯�������ֵΪ��0������B��Բ���˶�������ΪT�����B��A���������Цȳ������ֵ��ʼ��ʱ����BԶ��A�����Цȳ������ֵ������ʱ���õ�ʱ��Ϊ��������| A�� | $\frac{����-{��}_{0}��T}{�У�1-\sqrt{si{n}^{3}{��}_{0}}��}$ | B�� | $\frac{����-2{��}_{0}��T}{2�У�1-\sqrt{si{n}^{3}{��}_{0}}��}$ | ||
| C�� | $\frac{��2��-{��}_{0}��T}{2��1-\sqrt{si{n}^{3}{��}_{0}}��}$ | D�� | $\frac{��2��-{��}_{0}��T}{��1-\sqrt{si{n}^{3}{��}_{0}}��}$ |
���� �����Ƶ�����Բ���˶�������������������ǵĹ���뾶��ϵ��Ȼ��Ӧ�ÿ����յ���������������ǵ����ڹ�ϵ���������ת����Բ�Ľǣ�Ȼ��������ǵ��˶�ʱ�䣮
��� �⣺��AB��������B���ǹ������ʱ��A��B������A��O����ļн�����ɼ���֪ʶ�ɵã�RB=RAsin��0��
�ɿ����յ������ɵã�$\frac{{R}_{A}^{3}}{{T}_{A}^{2}}$=$\frac{{R}_{B}^{3}}{{T}_{B}^{2}}$������$\frac{{R}_{A}^{3}}{{T}_{A}^{2}}$=$\frac{��{R}_{A}^{\;}sin{��}_{0}��^{3}}{{T}^{2}}$����ã�TA=$\frac{T}{\sqrt{si{n}^{3}{��}_{0}}}$��
��B��A���������Цȳ������ֵ��ʼ��ʱ��BԶ��A�����Цȳ������ֵ���������У�
����ת����Բ�Ľǣ���=2��$\frac{��}{2}$-��0��=��-2��0����˹�������ʱ��Ϊt��
��$\frac{2��}{{T}_{B}}$-$\frac{2��}{{T}_{A}}$��t=�գ���ã�t=$\frac{����-2{��}_{0}��T}{2�У�1-\sqrt{si{n}^{3}{��}_{0}}��}$��
��ѡ��B��
���� ���⿼���������ǵ��˶�ʱ�����⣬�ܸ�����Ŀ��������Ϣ�����ӽ����ʱ�İ뾶��������Բ���˶����漰���ι�ϵ��뾶��һ�����������⣮

 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�| A�� | ʹ���ѹ�ӱ� | B�� | ʹ���ѹ���� | C�� | ʹ�����ӱ� | D�� | ʹ�������� |
| A�� | ���κι��Բο�ϵ�У���ѧ���ɶ���һ���ģ���һ���۳�Ϊ����˹̹�����ԭ�� | |
| B�� | �����Ϊc����ô����0.5c�˶��ɴ������κη�����Ĺ��ٶ���ȻΪc | |
| C�� | ���˹Τ��������Ԥ���˵�Ų��Ĵ��ڣ�����ͨ��ʵ��֤ʵ�˵�Ų��Ĵ��� | |
| D�� | �仯�ĵ糡һ��������Ų� |
| A�� | ��ʱ�ٶȵĴ�С��$\sqrt{5}$v0 | B�� | �˶���ʱ����$\frac{2{v}_{0}}{g}$ | ||
| C�� | ��ֱ���ٶȵĴ�С����2v0 | D�� | �˶���λ����$\frac{\sqrt{2}{v}_{0}^{2}}{g}$ |
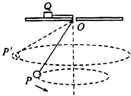 ��ͼ��ʾ��һ��ϸ���¶�˩һ������С��P��ϸ�ߵ��϶˹̶��ڽ�����Q�ϣ�Q���ڴ�С�ף�С�⻬���Ĺ̶�ˮƽ�����ϣ�С����ijһˮƽ����������Բ���˶���Բ�ڣ�����ʹС��ĵ�һ������һЩ��ˮƽ����������Բ���˶���ͼ��P��λ�ã������ν�����Q����ֹ�������ϵ�ͬһ�㣬���һ�������ԭ����Ƚϣ�������ж�����ȷ���ǣ�������
��ͼ��ʾ��һ��ϸ���¶�˩һ������С��P��ϸ�ߵ��϶˹̶��ڽ�����Q�ϣ�Q���ڴ�С�ף�С�⻬���Ĺ̶�ˮƽ�����ϣ�С����ijһˮƽ����������Բ���˶���Բ�ڣ�����ʹС��ĵ�һ������һЩ��ˮƽ����������Բ���˶���ͼ��P��λ�ã������ν�����Q����ֹ�������ϵ�ͬһ�㣬���һ�������ԭ����Ƚϣ�������ж�����ȷ���ǣ�������| A�� | ϸ�����ܵ�������С | B�� | С��P�˶��Ľ��ٶȱ�С | ||
| C�� | Q�ܵ������֧������� | D�� | Q�ܵ�����ľ�Ħ������� |
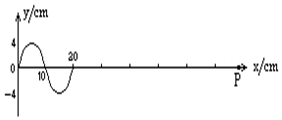 һ�кᲨ�IJ�Դ����ͼ�е�����ԭ��O��������0.4s����O�����Ҵ���20cm��P����O��ľ�����80cm����
һ�кᲨ�IJ�Դ����ͼ�е�����ԭ��O��������0.4s����O�����Ҵ���20cm��P����O��ľ�����80cm����