题目内容
19.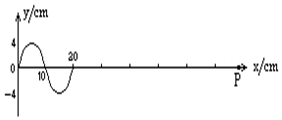 一列横波的波源在如图中的坐标原点O处,经过0.4s,振动从O点向右传播20cm,P点离O点的距离是80cm.求:
一列横波的波源在如图中的坐标原点O处,经过0.4s,振动从O点向右传播20cm,P点离O点的距离是80cm.求:(1)P点起振时的速度方向如何?
(2)该波从原点向右传播时开始计时,经多长时间质点P第一次到达波峰?(保留一位小数)
分析 (1)波传播的过程中,介质中各个质点的起振方向相同.振动从O点向右传播,x=20cm处质点的振动方向沿y轴负方向,即可知道P点起振时的速度方向沿y轴负方向.
(2)当图示x=5cm处的波峰传到P点时,质点P第一次到达波峰.由题经过0.4s,振动从O点向右传播20cm,求出波速,再求出质点P第一次到达波峰所经过的时间.
解答 解:(1)振动从O点向右传播,根据“上下坡法”可知,x=20cm处质点的起振方向沿y轴负方向,则P点起振时的速度方向沿y轴负方向.
(2)经过0.4s,振动从O点向右传播20cm,可得波速 v=$\frac{x}{t}$=$\frac{0.2}{0.4}$=0.5m/s.x=5cm处的振动状态传到P点时波传播的距离 x=75cm=0.75m,则质点P第一次到达波峰所经过的时间为 t=$\frac{x}{v}$+0.4s=$\frac{0.75}{0.5}$s+0.4s=1.9s.
答:
(1)P点起振时的速度方向沿y轴负方向.
(2)该波从原点向右传播时开始计时,经1.9s时间质点P第一次到达波峰.
点评 本题解题时,要抓住波的基本特点:介质中各质点的起振方向与波源的起振方向相同,知道波在同一均匀介质中是匀速传播的.运用波形平移法研究第2问,也可以分过程求时间.

练习册系列答案
相关题目
18.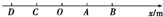 某一运动质点沿一直线做往返运动,如图所示,OA=AB=OC=CD=1m,O点为x轴上的原点,且质点由A点出发向x轴的正方向运动至B点再返回沿x轴的负方向运动,以下说法正确的是( )
某一运动质点沿一直线做往返运动,如图所示,OA=AB=OC=CD=1m,O点为x轴上的原点,且质点由A点出发向x轴的正方向运动至B点再返回沿x轴的负方向运动,以下说法正确的是( )
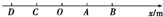 某一运动质点沿一直线做往返运动,如图所示,OA=AB=OC=CD=1m,O点为x轴上的原点,且质点由A点出发向x轴的正方向运动至B点再返回沿x轴的负方向运动,以下说法正确的是( )
某一运动质点沿一直线做往返运动,如图所示,OA=AB=OC=CD=1m,O点为x轴上的原点,且质点由A点出发向x轴的正方向运动至B点再返回沿x轴的负方向运动,以下说法正确的是( )| A. | 质点在A→B→C的时间内发生的位移为2 m,方向沿x轴正方向,路程为4 m | |
| B. | 质点在B→D的时间内发生的位移为-4 m,方向沿x轴负方向,路程为4 m | |
| C. | 当质点到达D点时,其位置可用D点的坐标-2 m表示 | |
| D. | 当质点到达D点时,相对于A点的位移为-3 m |
7.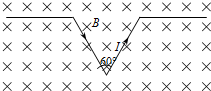 长为4L的直导线等分成四等份,拆成如图所示的图形,其中的V形导线夹角为60°,整个图形置于与其所在平面相垂直的匀强磁场中,磁场的磁感应强度为B,当在该导线中通以大小为I的电流时,该V形通电导线受到的安培力大小为( )
长为4L的直导线等分成四等份,拆成如图所示的图形,其中的V形导线夹角为60°,整个图形置于与其所在平面相垂直的匀强磁场中,磁场的磁感应强度为B,当在该导线中通以大小为I的电流时,该V形通电导线受到的安培力大小为( )
 长为4L的直导线等分成四等份,拆成如图所示的图形,其中的V形导线夹角为60°,整个图形置于与其所在平面相垂直的匀强磁场中,磁场的磁感应强度为B,当在该导线中通以大小为I的电流时,该V形通电导线受到的安培力大小为( )
长为4L的直导线等分成四等份,拆成如图所示的图形,其中的V形导线夹角为60°,整个图形置于与其所在平面相垂直的匀强磁场中,磁场的磁感应强度为B,当在该导线中通以大小为I的电流时,该V形通电导线受到的安培力大小为( )| A. | BIL | B. | 2BIL | C. | 3BIL | D. | 4BIL |
14.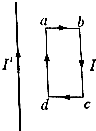 长方形线框abcd通有恒定电流I,在线框所在平面内线框的左侧与ad边平行放置一长直导线,导线中通有恒定电流I′,电流的方向如图所示,线框和长直导线的位置都被固定,下列关于线框受到安培力的说法中正确的是( )
长方形线框abcd通有恒定电流I,在线框所在平面内线框的左侧与ad边平行放置一长直导线,导线中通有恒定电流I′,电流的方向如图所示,线框和长直导线的位置都被固定,下列关于线框受到安培力的说法中正确的是( )
 长方形线框abcd通有恒定电流I,在线框所在平面内线框的左侧与ad边平行放置一长直导线,导线中通有恒定电流I′,电流的方向如图所示,线框和长直导线的位置都被固定,下列关于线框受到安培力的说法中正确的是( )
长方形线框abcd通有恒定电流I,在线框所在平面内线框的左侧与ad边平行放置一长直导线,导线中通有恒定电流I′,电流的方向如图所示,线框和长直导线的位置都被固定,下列关于线框受到安培力的说法中正确的是( )| A. | 线框的ab和cd边不受安培力 | |
| B. | 线框所受的安培力合力向右 | |
| C. | 线框所受的安培力合力向左 | |
| D. | 若长直导线的电流I′加倍,则稳定后线框所受的安培力合力也随之加倍 |
4.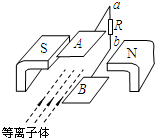 目前世界上正在研究的一种新型发电机叫磁流体发电机,图11表示它的发电原理:将一束等离子体(即高温下电离的气体,含有大量带正电和带负电的微粒,而从整体上来说呈电中性)喷入磁场,由于等离子体在磁场力的作用下运动方向发生偏转,磁场中的两块金属板A和B上就会聚集电荷,从而在两板间产生电压.在图示磁极配置的情况下,金属板的电势高低和通过电阻R的电流方向分别是( )
目前世界上正在研究的一种新型发电机叫磁流体发电机,图11表示它的发电原理:将一束等离子体(即高温下电离的气体,含有大量带正电和带负电的微粒,而从整体上来说呈电中性)喷入磁场,由于等离子体在磁场力的作用下运动方向发生偏转,磁场中的两块金属板A和B上就会聚集电荷,从而在两板间产生电压.在图示磁极配置的情况下,金属板的电势高低和通过电阻R的电流方向分别是( )
 目前世界上正在研究的一种新型发电机叫磁流体发电机,图11表示它的发电原理:将一束等离子体(即高温下电离的气体,含有大量带正电和带负电的微粒,而从整体上来说呈电中性)喷入磁场,由于等离子体在磁场力的作用下运动方向发生偏转,磁场中的两块金属板A和B上就会聚集电荷,从而在两板间产生电压.在图示磁极配置的情况下,金属板的电势高低和通过电阻R的电流方向分别是( )
目前世界上正在研究的一种新型发电机叫磁流体发电机,图11表示它的发电原理:将一束等离子体(即高温下电离的气体,含有大量带正电和带负电的微粒,而从整体上来说呈电中性)喷入磁场,由于等离子体在磁场力的作用下运动方向发生偏转,磁场中的两块金属板A和B上就会聚集电荷,从而在两板间产生电压.在图示磁极配置的情况下,金属板的电势高低和通过电阻R的电流方向分别是( )| A. | A板电势高,电流方向a→b | B. | A板电势高,电流方向b→a | ||
| C. | B板电势高,电流方向a→b | D. | B板电势高,电流方向b→a |
8. 如图所示为速度选择器原理示意图,匀强磁场的方向垂直纸面向里,磁感应强度为B,匀强电场的方向沿纸面向下,电场强度为E,一个正一价离子(离子的重力很小,忽略不计)以速度v0沿直线O1O2运动,从孔O2出电磁场,则下述判断正确的是( )
如图所示为速度选择器原理示意图,匀强磁场的方向垂直纸面向里,磁感应强度为B,匀强电场的方向沿纸面向下,电场强度为E,一个正一价离子(离子的重力很小,忽略不计)以速度v0沿直线O1O2运动,从孔O2出电磁场,则下述判断正确的是( )
 如图所示为速度选择器原理示意图,匀强磁场的方向垂直纸面向里,磁感应强度为B,匀强电场的方向沿纸面向下,电场强度为E,一个正一价离子(离子的重力很小,忽略不计)以速度v0沿直线O1O2运动,从孔O2出电磁场,则下述判断正确的是( )
如图所示为速度选择器原理示意图,匀强磁场的方向垂直纸面向里,磁感应强度为B,匀强电场的方向沿纸面向下,电场强度为E,一个正一价离子(离子的重力很小,忽略不计)以速度v0沿直线O1O2运动,从孔O2出电磁场,则下述判断正确的是( )| A. | 速度大小v0=$\frac{E}{B}$ | |
| B. | 沿O1O2进场,速度v>$\frac{E}{B}$的正二价离子一定向上偏转 | |
| C. | 沿O1O2进场,速度v=$\frac{E}{B}$的负离子一定向上偏转 | |
| D. | 若离子逆向运动,沿O2O1进场,速度v=$\frac{E}{B}$的离子一定是直线运动 |
9.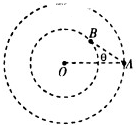 如图所示,人造卫星A、B在同一平面内绕地心O做同向的匀速圆周运动.A、B连线与A、O连线间的夹角θ随时间发生变化,且最大值为θ0,卫星B做圆周运动的周期为T,则从B向A靠近过程中θ出现最大值开始计时,到B远离A过程中θ出现最大值结束计时所用的时间为( )
如图所示,人造卫星A、B在同一平面内绕地心O做同向的匀速圆周运动.A、B连线与A、O连线间的夹角θ随时间发生变化,且最大值为θ0,卫星B做圆周运动的周期为T,则从B向A靠近过程中θ出现最大值开始计时,到B远离A过程中θ出现最大值结束计时所用的时间为( )
 如图所示,人造卫星A、B在同一平面内绕地心O做同向的匀速圆周运动.A、B连线与A、O连线间的夹角θ随时间发生变化,且最大值为θ0,卫星B做圆周运动的周期为T,则从B向A靠近过程中θ出现最大值开始计时,到B远离A过程中θ出现最大值结束计时所用的时间为( )
如图所示,人造卫星A、B在同一平面内绕地心O做同向的匀速圆周运动.A、B连线与A、O连线间的夹角θ随时间发生变化,且最大值为θ0,卫星B做圆周运动的周期为T,则从B向A靠近过程中θ出现最大值开始计时,到B远离A过程中θ出现最大值结束计时所用的时间为( )| A. | $\frac{(π-{θ}_{0})T}{π(1-\sqrt{si{n}^{3}{θ}_{0}})}$ | B. | $\frac{(π-2{θ}_{0})T}{2π(1-\sqrt{si{n}^{3}{θ}_{0}})}$ | ||
| C. | $\frac{(2π-{θ}_{0})T}{2π(1-\sqrt{si{n}^{3}{θ}_{0}})}$ | D. | $\frac{(2π-{θ}_{0})T}{π(1-\sqrt{si{n}^{3}{θ}_{0}})}$ |