题目内容
5. 质量为m的钢珠从高出沙坑表面H米处由静止自由下落,不考虑空气阻力,掉入沙坑后停止,如图所示,已知钢珠在沙坑中受到沙的平均阻力是f,则钢珠在沙内运动时间为多少?
质量为m的钢珠从高出沙坑表面H米处由静止自由下落,不考虑空气阻力,掉入沙坑后停止,如图所示,已知钢珠在沙坑中受到沙的平均阻力是f,则钢珠在沙内运动时间为多少?
分析 由自由落体规律可求得钢珠在空中运动的时间,再对全程由动量定理可求得在沙内运动的时间.
解答 解:由H=$\frac{1}{2}$gt2可得:
钢珠在空中运动的时间t=$\sqrt{\frac{2H}{g}}$
设向下为正方向,对全程进行分析由动量定理可知;
mg(t+t′)-ft′=0
解得:t′=$\frac{mg}{f-mg}\sqrt{\frac{2H}{g}}$
答:钢珠在沙内运动时间为$\frac{mg}{f-mg}\sqrt{\frac{2H}{g}}$
点评 本题考查动量定理的应用,要注意明确动量定理中的矢量性,同时要注意对全程进行分析列动量定理的表达式更简单.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
15.重量为20N的物体除受到重力外,还受到另外两个力的作用而静止,已知它受到的其中一个外力F1=10N,则另外一个外力F2的大小可能是( )
| A. | 5N | B. | 8N | C. | 10$\sqrt{3}$N | D. | 20N |
20. 如图所示,静止的小球沿不同的轨道由同一位置滑到水平桌面上,轨道高度为h,桌面距地面高为H,物体质量为m则以下说法正确的是( )
如图所示,静止的小球沿不同的轨道由同一位置滑到水平桌面上,轨道高度为h,桌面距地面高为H,物体质量为m则以下说法正确的是( )
 如图所示,静止的小球沿不同的轨道由同一位置滑到水平桌面上,轨道高度为h,桌面距地面高为H,物体质量为m则以下说法正确的是( )
如图所示,静止的小球沿不同的轨道由同一位置滑到水平桌面上,轨道高度为h,桌面距地面高为H,物体质量为m则以下说法正确的是( )| A. | 小球沿三种不同轨道下滑到桌面上的过程,重力做功一样多 | |
| B. | 小球沿曲线轨道下滑到桌面上的过程,重力做功最多 | |
| C. | 以桌面为参考面,小球的重力势能的减少量为mgh | |
| D. | 以地面为参考面,小球的重力势能的减少量为mg(H+h) |
17.在物理学发展的过程中,有许多伟大的科学家做出了突出贡献,关于科学家和他们的贡献,下列说法正确的是( )
| A. | 伽利略通过“理想实验”得出结论:运动必具有一定速度,如果它不受力,它将以这一速度永远运动下去 | |
| B. | 德国天文学家开普勒对他导师第谷观测的行星数据进行多年研究,得出了万有引力定律 | |
| C. | 牛顿发现了万有引力定律,卡文迪许通过实验测出了引力常量 | |
| D. | 古希腊学者亚里士多德认为物体下落快慢由它们的重量决定,牛顿利用逻辑推断使亚里士多德的理论陷入了困境 |
8. 如图所示,OA为一条遵循胡克定律的弹性轻绳,弹性轻绳的一端固定在O点,另一端拴一个物体,物体静止在水平面上,并对水平面有压力.B处有一光滑的钉子且与OA垂直,OB为弹性绳子的自然长度,BA的高度为h.现在,用水平力F使物体沿水平面匀速运动,这一过程中,设水平面对物体的摩擦力的大小为f,对物体的支持力为N.则( )
如图所示,OA为一条遵循胡克定律的弹性轻绳,弹性轻绳的一端固定在O点,另一端拴一个物体,物体静止在水平面上,并对水平面有压力.B处有一光滑的钉子且与OA垂直,OB为弹性绳子的自然长度,BA的高度为h.现在,用水平力F使物体沿水平面匀速运动,这一过程中,设水平面对物体的摩擦力的大小为f,对物体的支持力为N.则( )
 如图所示,OA为一条遵循胡克定律的弹性轻绳,弹性轻绳的一端固定在O点,另一端拴一个物体,物体静止在水平面上,并对水平面有压力.B处有一光滑的钉子且与OA垂直,OB为弹性绳子的自然长度,BA的高度为h.现在,用水平力F使物体沿水平面匀速运动,这一过程中,设水平面对物体的摩擦力的大小为f,对物体的支持力为N.则( )
如图所示,OA为一条遵循胡克定律的弹性轻绳,弹性轻绳的一端固定在O点,另一端拴一个物体,物体静止在水平面上,并对水平面有压力.B处有一光滑的钉子且与OA垂直,OB为弹性绳子的自然长度,BA的高度为h.现在,用水平力F使物体沿水平面匀速运动,这一过程中,设水平面对物体的摩擦力的大小为f,对物体的支持力为N.则( )| A. | f不变,N变小,F变大 | B. | f、N不变,F变大 | ||
| C. | f变小,N变小,F变大 | D. | 条件不够,无法判断 |
9. 如图所示,在水平地面上叠放着A、B、C三个完全相同的物块,今用水平力F作用于B时,A、B、C均处于静止状态,则不正确的是( )
如图所示,在水平地面上叠放着A、B、C三个完全相同的物块,今用水平力F作用于B时,A、B、C均处于静止状态,则不正确的是( )
 如图所示,在水平地面上叠放着A、B、C三个完全相同的物块,今用水平力F作用于B时,A、B、C均处于静止状态,则不正确的是( )
如图所示,在水平地面上叠放着A、B、C三个完全相同的物块,今用水平力F作用于B时,A、B、C均处于静止状态,则不正确的是( )| A. | 地面对C的摩擦力等于F | B. | A对B的摩擦力等于$\frac{F}{2}$ | ||
| C. | B对A的摩擦力等于零 | D. | B对C的摩擦力等于F方向向右 |
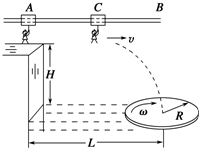 湖南卫视推出了大型户外竞技类节目《快乐向前冲》,是体力与耐力展现的一个体能竞赛活动.节目的场地设施如图所示,AB为水平直轨道,上面安装有电动悬挂器,可以载人运动,水面上漂浮着一个半径为R、角速度为ω、铺有海绵垫的转盘,转盘的轴心离平台的水平距离为L,平台边缘与转盘平面的高度差为H.选手抓住悬挂器可以在电动机的带动下,从A点下方的平台边缘处沿水平方向做初速度为零、加速度为a的匀加速直线运动.选手必须作好判断,在合适的位置释放,才能顺利落在转盘上.设人的质量为m(不计身高),人与转盘间的最大静摩擦力为μmg,重力加速度为g.
湖南卫视推出了大型户外竞技类节目《快乐向前冲》,是体力与耐力展现的一个体能竞赛活动.节目的场地设施如图所示,AB为水平直轨道,上面安装有电动悬挂器,可以载人运动,水面上漂浮着一个半径为R、角速度为ω、铺有海绵垫的转盘,转盘的轴心离平台的水平距离为L,平台边缘与转盘平面的高度差为H.选手抓住悬挂器可以在电动机的带动下,从A点下方的平台边缘处沿水平方向做初速度为零、加速度为a的匀加速直线运动.选手必须作好判断,在合适的位置释放,才能顺利落在转盘上.设人的质量为m(不计身高),人与转盘间的最大静摩擦力为μmg,重力加速度为g.