题目内容
13.有一架电梯静止于底楼,启动时以2m/s2的加速度匀加速上升,制动时以-1m/s2的加速度匀减速上升,到达楼顶时上升的总高度为52m.问:(1)如果电梯先匀加速上升,然后匀速上升,最后匀减速上升,到楼顶全程共用时间为16s,上升的最大速度是多少?
(2)若电梯上升的最大速度为8m/s,电梯升到楼顶的最短时间是多少?
分析 (1)根据匀变速直线运动的平均速度推论,结合运动学公式,抓住总位移、总时间,求出上升的最大速度.
(2)根据速度时间公式求出匀加速和匀减速运动的时间,根据速度位移公式求出匀加速和匀减速运动的位移,从而得出匀速运动的位移,求出匀速运动的时间,从而得出总时间.
解答 解:(1)设最大速度为v,根据平均速度推论知,总位移为:
x=$\frac{v}{2}{t}_{1}+v{t}_{2}+\frac{v}{2}{t}_{3}$=52m,
t1+t2+t3=16s,
又v=a1t1,v=-a2t3,
代入数据,联立解得v=4m/s.
(2)匀加速运动的时间为:${t}_{1}=\frac{{v}_{m}}{{a}_{1}}=\frac{8}{2}s=4s$,
匀减速运动的时间为:${t}_{3}=\frac{-{v}_{m}}{{a}_{2}}=\frac{-8}{-1}s$=8s,
匀加速运动的位移为:${x}_{1}=\frac{{{v}_{m}}^{2}}{2{a}_{1}}=\frac{64}{4}m=16m$,
匀减速运动的位移为:${x}_{3}=\frac{-{{v}_{m}}^{2}}{2{a}_{2}}=\frac{64}{-2}m=32m$,
则匀速运动的时间为:${t}_{3}=\frac{x-{x}_{1}-{x}_{3}}{{v}_{m}}=\frac{52-16-32}{8}s=0.5s$,
电梯升到楼顶的最短时间为:t=t1+t2+t3=4+0.5+8s=12.5s.
答:(1)上升的最大速度是4m/s;
(2)电梯升到楼顶的最短时间是12.5s.
点评 解决本题的关键理清电梯的运动过程,抓住总位移一定,灵活运用运动学公式进行求解.

练习册系列答案
相关题目
3. 如图所示,圆形线圈共n匝,线圈平面与磁场方向夹600角,匀强磁场磁感应为B,采用下列哪种方式能使线圈中磁通量变为原来的2倍( )
如图所示,圆形线圈共n匝,线圈平面与磁场方向夹600角,匀强磁场磁感应为B,采用下列哪种方式能使线圈中磁通量变为原来的2倍( )
 如图所示,圆形线圈共n匝,线圈平面与磁场方向夹600角,匀强磁场磁感应为B,采用下列哪种方式能使线圈中磁通量变为原来的2倍( )
如图所示,圆形线圈共n匝,线圈平面与磁场方向夹600角,匀强磁场磁感应为B,采用下列哪种方式能使线圈中磁通量变为原来的2倍( )| A. | 使线圈面积变为原来的2倍 | B. | 使线圈匝数变为原来的2倍 | ||
| C. | 使线圈半径变为原来的2倍 | D. | 使线圈平面与磁场垂直 |
4.许多科学家在物理学发展过程中做出了重要贡献.下列表述正确的是( )
| A. | 卡文迪许测出引力常数 | |
| B. | 安培发现电磁感应现象 | |
| C. | 奥斯特提出了磁场对运动电荷的作用力公式 | |
| D. | 法拉第总结并确认了真空中静止点电荷之间相互作用规律 |
1.如图画的是两个由同一起点向同一方向作直线运动的物体的速度图象.( )
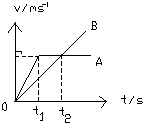

| A. | 到t1时刻A停下 | B. | 到t2时刻B追上A | ||
| C. | 0~t1时间内A的加速度小 | D. | 0~t2时间内A一直在B前方 |
18.如图所示,一个小球m用细绳系着在水平面上作匀速圆周运动.小球在转动的过程中( )


| A. | 受到拉力、重力、向心力 | B. | 重力做功为0 | ||
| C. | 处于平衡状态 | D. | 拉力做了正功 |
2.下列说法正确的是( )
| A. | 卢瑟福通过α粒子散射实验证实了在原子核内部存在质子 | |
| B. | 铀核(${\;}_{92}^{238}$U)衰变为铅核(${\;}_{82}^{206}$Pb)的过程中,要经过8次α衰变和6次β衰变 | |
| C. | 按照爱因斯坦的理论,在光电效应中,金属中的电子吸收一个光子获得的能量是hv,这些能量的一部分用来克服金属的逸出功W0,剩下的表现为逸出后电子的初动能Ek | |
| D. | 玻尔的原子理论第一次将量子观念引入原子领域,提出了定态和跃迁的概念,成功地解释了所有原子光谱的实验规律 | |
| E. | 铀核(${\;}_{92}^{238}$U)衰变成α离子和另一原子核,衰变产物的结合能之和一定大于铀核的结合能 |
 近年来,智能手机的普及使“低头族”应运而生.近日研究发现,玩手机时,就有可能让颈椎承受多达60磅(约270N)的重量,相当干给颈椎挂俩大西瓜,比一个7岁小孩还重.不当的姿势与一系列健康问题存在关联,如背痛、体重增加、胃痛、偏头痛和呼吸道疾病等.当人体直立时,颈椎所承受的压力等于头部的重量;但当低头时,颈椎受到的压力会随之变化.现将人体头颈部简化为如图的模型:重心在P点的头部,在可绕O转动的颈椎OP(轻杆)的支持力和沿PQ方向肌肉拉力的作用下处于静止.当低头时,颈椎与竖直方向的夹角为45°,PQ与竖直方向的夹角为53°,此时,颈椎受到的压力约为直立时颈椎受到压力的( )(sin37°=0.6,cos37°=0.8,sin45°=cos45°=$\frac{{\sqrt{2}}}{2}$,g=10m/2).
近年来,智能手机的普及使“低头族”应运而生.近日研究发现,玩手机时,就有可能让颈椎承受多达60磅(约270N)的重量,相当干给颈椎挂俩大西瓜,比一个7岁小孩还重.不当的姿势与一系列健康问题存在关联,如背痛、体重增加、胃痛、偏头痛和呼吸道疾病等.当人体直立时,颈椎所承受的压力等于头部的重量;但当低头时,颈椎受到的压力会随之变化.现将人体头颈部简化为如图的模型:重心在P点的头部,在可绕O转动的颈椎OP(轻杆)的支持力和沿PQ方向肌肉拉力的作用下处于静止.当低头时,颈椎与竖直方向的夹角为45°,PQ与竖直方向的夹角为53°,此时,颈椎受到的压力约为直立时颈椎受到压力的( )(sin37°=0.6,cos37°=0.8,sin45°=cos45°=$\frac{{\sqrt{2}}}{2}$,g=10m/2). 质量为m的钢珠从高出沙坑表面H米处由静止自由下落,不考虑空气阻力,掉入沙坑后停止,如图所示,已知钢珠在沙坑中受到沙的平均阻力是f,则钢珠在沙内运动时间为多少?
质量为m的钢珠从高出沙坑表面H米处由静止自由下落,不考虑空气阻力,掉入沙坑后停止,如图所示,已知钢珠在沙坑中受到沙的平均阻力是f,则钢珠在沙内运动时间为多少? 如下图所示,一平行板电容器板长L=4cm,板间距离d=3cm,倾斜放置,使板面与水平方向夹角α=37°,若两板间所加电压U=100V,一带电荷量Q=3×10-10C的负电荷以v0=0.5m•s-1的速度自A板左边缘水平进入电场,在电场中沿水平方向运动,并恰好从B板右边缘水平飞出,则:(g=10m/s2)
如下图所示,一平行板电容器板长L=4cm,板间距离d=3cm,倾斜放置,使板面与水平方向夹角α=37°,若两板间所加电压U=100V,一带电荷量Q=3×10-10C的负电荷以v0=0.5m•s-1的速度自A板左边缘水平进入电场,在电场中沿水平方向运动,并恰好从B板右边缘水平飞出,则:(g=10m/s2)