题目内容
【题目】如图所示，在平面直角坐标系xoy的第一象限内有一直角边长为L的等腰直角三角形OPQ，三角形的O点恰好为平面直角坐标系xoy的坐标原点该区域内有磁感应强度为B、方向垂直于纸面向里的匀强磁场，第一象限中y≤L的其它区域内有大小为E、方向沿x轴正方向的匀强电场；一束电子（电荷量为-e、质量为m）以大小不同的初速度从坐标原点O沿y轴正方向射入匀强磁场区域。则：
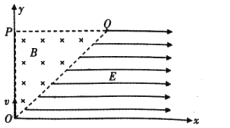
（1）能够进入电场区域的电子，初速度大小范围是多少；
（2）已知一个电子能从OQ之间某一点进入电场区域，最后恰好从P点离开磁场，求该电子由O到P的运动时间；
（3）若电场区域的电场强度E大小连续可调，要使电子能从x轴离开电场，则电子的初速度v大小和电场强度E大小分别满足什么条件。
【答案】（1）0≤v≤
（2）
+
；（3）v≤
，E≤
【解析】
（1）通过Q点进入电场区域的电子速度最大，其半径r1=L
由牛顿第二定律得：ev1B=m
解得：v1=
能够进入电场区域的电子的速度范围是：0≤v≤
（2）设从P点离开磁场的电子半径为r2，则有：r2=
由牛顿第二定律得：ev2B=m
解得：v2=
因为电子在磁场运动的周期为：T=
电子第一次和第二次穿过磁场的时间相等，均为
个周期，即为：t1=t2=
=
在电场中运动：由牛顿第二定律得：eE=ma
电子在电场中的运动时间为：t3=2×
联立解得：t3=
所以，电子由O到P的运动时间为：t=t1+t2+t3=
+；
（3）只有当电子第一次从电场回到磁场且不从OP和PQ两边离开磁场时，电子才有可能偏转通过x轴，即电子第一次返回磁场的半径r3满足； r3
设电子从O点射入的初速度为v3，根据洛伦兹力提供向心力可得：ev3B=
解得：v3≤
电子第二次进入电场的坐标x=2r3，y=2r3，
电子经过电场偏转到达x轴的时间： t=
=
到达x轴时沿x轴负方向的位移x0=
=
当x0≤2r3时，即可由电子穿过x轴，因r3，则
得：E≤
要使电子能从x轴离开电场，则电子的初速度条件为：v≤，电场强度条件为：E≤.
