��Ŀ����
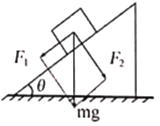
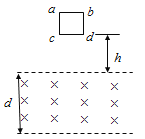
����Ŀ����ͼ��ʾ���綯���������Ϊ����37��Ĵ��ʹ���v��8m/s���ٶ���ʱ�������˶������ʹ��¶˵�C��ˮƽ��CDPƽ�����ӣ�B��C���L��20m�����ʹ����϶˵�Bǡ����̶�����ֱƽ���ڵİ뾶ΪR��0.5m�Ĺ⻬Բ��������У�һ���ʵ��ɵ��Ҷ˹̶���P���ĵ����ϣ�����M��2kg�ɿ����ʵ�����忿�ڵ��ɵ����D������ʱ���ɴ���ԭ����C��D���x��1m��PD�ι⻬��DC�δֲ��ֽ�Mѹ������һ��������ɾ�ֹ�ͷţ�M����DC���ϴ��ʹ�����B����Ϲ⻬Բ�¹����ͨ����ߵ�Aʱ��A���ѹ��Ϊ8N�����������У�M��C�㻬�ϴ��ʹ�ʱ���ٶȴ�С���䣬�����Ϊ�ش��ʹ�������֪�봫�ʹ�ͬ�Ķ�Ħ������Ϊ����0.8����CD�μ�Ķ�Ħ������Ϊ����0.5���������ٶȴ�Сg��10m/s2����
��1����Բ�������B��ʱ������ٶ�
��2��M�ڴ��ʹ����˶��Ĺ����У��������ʹ��ĵ綯����������M������ĵ���E��
��3��M�ͷ�ǰ��ϵͳ���еĵ�������Ep

���𰸡���1��5.0m/s��2��512J����3��19J
��������
��1��Mǡ�ܹ�A�㣬��ţ�ٵڶ����ɣ�Mg+FA��M![]()
���vA��![]() m/s��
m/s��
��B��A�ɻ�е���غ㣺��Mg��R+Rcos������![]()
���vB��5.0m/s
��2��M�ڴ��ʹ����˶�ʱ����vBС��Ƥ���ٶȣ���֪����һֱ�������˶���
����1Mgcos����Mgsin����Ma
���a��0.4m/s2
�ɹ�ʽ��vB2-vC2��2aL�����v��3m/s
��vB��vC+at���t��5s��
���ʹ���tʱ���ڵ�λ�ƣ�x1��vt��40m��
���������Ƥ������Ƥ�����µ�Ħ������Ҫά��Ƥ�������˶����ʵ綯��Ҫ�����Ƥ��һ����Ƥ�����ϵ�ǣ��������С�������ܵ���Ħ����һ����
�����Ĺ�W����Mgcos��x1��512J��������ĵ���E��512J
��3���赯�ɵ�������������W����ӵ��ɵ�ѹ���˵�C�㣬��M�ɶ��ܶ�����
W����2Mgx0��![]() MvC2��0
MvC2��0
��ã�W��19J
��֪Ep��19J