题目内容
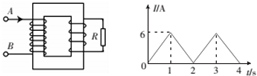
5.如图甲所示的装置叫做阿特伍德机,是英国数学家和物理学家阿特伍德创制的一种著名力学实验装置,用来研究匀变速直线运动的规律.某同学对该装置加以改进后用来验证机械能守恒定律,如图乙所示.
(1)实验时,该同学进行了如下步骤:
①将质量均为M(A的含挡光片、B的含挂钩)的重物用绳连接后,跨放在定滑轮上,处于静止状态,测量出挡光片中心(填“A的上表面”、“A的下表面”或“挡光片中心”)到光电门中心的竖直距离h.
②在B的下端挂上质量为m的物块C,让系统(重物A、B以及物块C)中的物体由静止开始运动,光电门记录挡光片挡光的时间为△t.
③测出挡光片的宽度d,计算有关物理量,验证机械能守恒定律.
(2)如果系统(重物A、B以及物块C)的机械能守恒,应满足的关系式为mgh=$\frac{1}{2}$(2M+m)($\frac{d}{△t}$)2(已知重力加速度为g)
(3)引起该实验系统误差的原因有绳子有质量;或滑轮与绳子有摩擦;或重物运动受到阻力作用(写一条即可).
(4)验证实验结束后,该同学突发奇想:如果系统(重物A、B以及物块C)的机械能守恒,不断增大物块C的质量m,重物B的加速度a也将不断增大,那么a与m之间有怎样的定量关系?a随m增大会趋于一个什么值?请你帮该同学解决:
①写出a与m之间的关系式:a=$\frac{mg}{2M+m}$(还要用到M和g);
②a的值会趋于重力加速度g.
分析 根据系统机械能守恒,得出系统重力势能的减小量和系统动能的增加量,根据极短时间内的平均速度表示瞬时速度求出系统末动能.
对系统研究,根据牛顿第二定律求出加速度与m的关系式,通过关系式分析,m增大,a趋向于何值.
解答 解:(1、2)需要测量系统重力势能的变化量,则应该测量出挡光片中心到光电门中心的距离,系统的末速度为:v=$\frac{d}{△t}$,
则系统重力势能的减小量△Ep=mgh,系统动能的增加量为:△Ek=$\frac{1}{2}$(2M+m)v2=$\frac{1}{2}$(2M+m)($\frac{d}{△t}$)2,
若系统机械能守恒,则有:mgh=$\frac{1}{2}$(2M+m)($\frac{d}{△t}$)2.
(3)系统机械能守恒的条件是只有重力做功,引起实验误差的原因可能有:绳子有一定的质量、滑轮与绳子之间有摩擦、重物运动受到空气阻力等.
(4)根据牛顿第二定律得,系统所受的合力为mg,则系统加速度为:a=$\frac{mg}{2M+m}$=$\frac{g}{\frac{2M}{m}+1}$,当m不断增大,则a趋向于g.
故答案为:(1)挡光片中心;
(2)mgh=$\frac{1}{2}(2M+m)(\frac{d}{△t})^{2}$;
(3)绳子有质量;滑轮与绳子有摩擦;重物运动受到阻力作用(回答一个即可);
(4)①a=$\frac{mg}{2M+m}$;②重力加速度g.
点评 解决本题的关键知道实验的原理,知道误差产生的原因,掌握整体法在牛顿第二定律中的运用.

练习册系列答案
相关题目
8.一物体作直线运动的速度图象如图所示,则下列说法错误的是( )
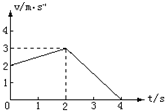

| A. | 前2s内做匀加速直线运动 | B. | 前4s内做匀变速直线运动 | ||
| C. | 前4s内的平均速度为2m/s | D. | 后2s内的加速度为-1.5m/s2 |
20.演示位移传感器的工作原理如图甲所示,物体M在导轨上平移时,带动滑动变阻器的金属杆P,通过理想电压表显示的数据来反映物体的位移x.设电源电动势为E,内阻不计,滑动变阻器的长度为L,物体M以O为平衡位置做简谐运动(取向右为正方向),振幅为$\frac{L}{2}$,物体经过O时P恰好位于滑动变阻器的中点,图乙是电压表的示数U随时间t的变化图象.关于t1时刻物体M的运动情况,下列说法正确的是( )
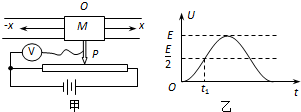

| A. | 物体M具有正方向的最大速度 | |
| B. | 物体M的速度为负方向且正在减小 | |
| C. | 物体M的加速度为零 | |
| D. | 物体M的加速度为负方向且正在增大 |
17. 如图所示为某游乐场的一个娱乐设施,图中的大转盘在竖直平面内匀速转动,坐在吊篮里的游人却显得悠然自得,对某个游人,下列说法正确的是( )
如图所示为某游乐场的一个娱乐设施,图中的大转盘在竖直平面内匀速转动,坐在吊篮里的游人却显得悠然自得,对某个游人,下列说法正确的是( )
 如图所示为某游乐场的一个娱乐设施,图中的大转盘在竖直平面内匀速转动,坐在吊篮里的游人却显得悠然自得,对某个游人,下列说法正确的是( )
如图所示为某游乐场的一个娱乐设施,图中的大转盘在竖直平面内匀速转动,坐在吊篮里的游人却显得悠然自得,对某个游人,下列说法正确的是( )| A. | 他所受合外力恰好为零 | |
| B. | 他所受合外力方向始终指向圆周运动圆心 | |
| C. | 他的机械能保持不变 | |
| D. | 他的机械能不断增加 |
15.下列各组选项中只含一个标量的选项是( )
| A. | 平均速度、质量、加速度 | B. | 瞬时速度、速率、路程 | ||
| C. | 平均速率、时间、温度 | D. | 频率、位移、速度 |
 如图所示是某矿井中的升降机由井底上升到井口的过程中的运动图象,试根据速度-时间图象回答下列问题:
如图所示是某矿井中的升降机由井底上升到井口的过程中的运动图象,试根据速度-时间图象回答下列问题:
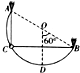 如图所示,将一质量为m的小环套在一半径为R的“半圆形”金属轨道上,并将轨道固定在竖直面内的A、B两点,直径AB与竖直半径OD夹角为60°.现将两根原长为R、劲度系数k=$\frac{mg}{R}$的弹性轻绳一端固定在小环上,另一端分别固定在A、B两点.已知弹性轻绳满足胡克定律,不计一切摩擦,重力加速度为g.将小环由A点正下方的C点静止释放,当小环运动到金属轨道的最低点D时,求:
如图所示,将一质量为m的小环套在一半径为R的“半圆形”金属轨道上,并将轨道固定在竖直面内的A、B两点,直径AB与竖直半径OD夹角为60°.现将两根原长为R、劲度系数k=$\frac{mg}{R}$的弹性轻绳一端固定在小环上,另一端分别固定在A、B两点.已知弹性轻绳满足胡克定律,不计一切摩擦,重力加速度为g.将小环由A点正下方的C点静止释放,当小环运动到金属轨道的最低点D时,求: