题目内容
10.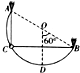 如图所示,将一质量为m的小环套在一半径为R的“半圆形”金属轨道上,并将轨道固定在竖直面内的A、B两点,直径AB与竖直半径OD夹角为60°.现将两根原长为R、劲度系数k=$\frac{mg}{R}$的弹性轻绳一端固定在小环上,另一端分别固定在A、B两点.已知弹性轻绳满足胡克定律,不计一切摩擦,重力加速度为g.将小环由A点正下方的C点静止释放,当小环运动到金属轨道的最低点D时,求:
如图所示,将一质量为m的小环套在一半径为R的“半圆形”金属轨道上,并将轨道固定在竖直面内的A、B两点,直径AB与竖直半径OD夹角为60°.现将两根原长为R、劲度系数k=$\frac{mg}{R}$的弹性轻绳一端固定在小环上,另一端分别固定在A、B两点.已知弹性轻绳满足胡克定律,不计一切摩擦,重力加速度为g.将小环由A点正下方的C点静止释放,当小环运动到金属轨道的最低点D时,求:(1)小环的速率v;
(2)金属轨道对小环的作用力F的大小.
分析 (1)对CD过程分析,根据机械能守恒定律可求得小环的速率v;
(2)由胡克定律求解AD段绳上的张力,再根据向心力公式进行分析即可明确小球受到的作用力大小.
解答 解:(1)在CD两点,弹性绳的弹性势能相等,由机械能守恒定律可得:
mg$\frac{R}{2}$=$\frac{1}{2}$mv2
得v=$\sqrt{gR}$;
(2)在D点,AD段弹性绳的伸长量x=($\sqrt{3}$-1)R,BD段弹性绳弹力为0,
所以AD段弹性绳张力T=kx=$\frac{mg}{R}$($\sqrt{3}$-1)R=($\sqrt{3}$-1)mg
在D点时,设导轨对圆环的作用力F是向上的支持力
由向心力公式可知:
($\sqrt{3}$-1)mgcos30°+F-mg=m$\frac{{v}^{2}}{R}$
解得:F=$\frac{1+\sqrt{3}}{2}$mg.
答:(1)小环的速率v为$\sqrt{gR}$;
(2)金属轨道对小环的作用力F的大小为$\frac{1+\sqrt{3}}{2}$mg.
点评 本题考查机械能守恒定律以及向心力公式的应用,要注意正确分析过程,并能正确进行受力分析,能正确利用向心力公式列式即可求解.

练习册系列答案
相关题目
1.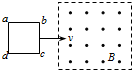 一个闭合矩形线圈abcd以速度v从无磁场区域匀速穿过匀强磁场区域,而再次进入无磁场区域,如图所示,设感应电流沿顺时针方向为正值,那么,下图中能正确反映线圈中电流-时间关系的图象是( )
一个闭合矩形线圈abcd以速度v从无磁场区域匀速穿过匀强磁场区域,而再次进入无磁场区域,如图所示,设感应电流沿顺时针方向为正值,那么,下图中能正确反映线圈中电流-时间关系的图象是( )
 一个闭合矩形线圈abcd以速度v从无磁场区域匀速穿过匀强磁场区域,而再次进入无磁场区域,如图所示,设感应电流沿顺时针方向为正值,那么,下图中能正确反映线圈中电流-时间关系的图象是( )
一个闭合矩形线圈abcd以速度v从无磁场区域匀速穿过匀强磁场区域,而再次进入无磁场区域,如图所示,设感应电流沿顺时针方向为正值,那么,下图中能正确反映线圈中电流-时间关系的图象是( )| A. | 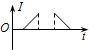 | B. | 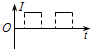 | C. | 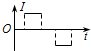 | D. | 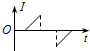 |
18.一只电炉的电阻丝和一台电动机线圈电阻相同,都为R.串联接在电路中(电动机正常运转),则以下说法正确的是( )
| A. | 电炉和电动机两端电压相等 | |
| B. | 电动机的电功率大于电炉的电功率 | |
| C. | 在相同的时间内电炉和电动机产生的电热相等 | |
| D. | 电炉两端电压与通过的电流的比值小于电动机两端电压与通过的电流的比值 |
15.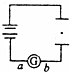 如图所示,将平行板电容器与电池相连,两板间的带电尘埃恰好处于静止状态.若将两板缓慢地错开一些,其他条件不变,则( )
如图所示,将平行板电容器与电池相连,两板间的带电尘埃恰好处于静止状态.若将两板缓慢地错开一些,其他条件不变,则( )
 如图所示,将平行板电容器与电池相连,两板间的带电尘埃恰好处于静止状态.若将两板缓慢地错开一些,其他条件不变,则( )
如图所示,将平行板电容器与电池相连,两板间的带电尘埃恰好处于静止状态.若将两板缓慢地错开一些,其他条件不变,则( )| A. | 电容器带电量不变 | B. | 尘埃仍静止 | ||
| C. | 电流计中有a→b的电流 | D. | 电流计中有b→a的电流 |
2.如图所示,金属棒向右平移时,下列说法正确的是( )
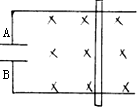

| A. | A极带负电,B极带正电 | B. | A极带正电,B极带负电 | ||
| C. | Ab棒上一定有电流 | D. | 极板不带电 |
19.关于电场中电荷的电势能的大小,下列说法正确的是( )
| A. | 在电场强度越大的地方,电荷的电势能也越大 | |
| B. | 正电荷沿电场线移动,电势能一定增大 | |
| C. | 负电荷沿电场线移动,电势能一定增大 | |
| D. | 正电荷沿电场线移动,电势能一定减小 |
20.某物体从桌面自由下落,经过离地面高为0.8m的位置时,速度是落地速度的$\frac{3}{5}$,g取10m/s2,则( )
| A. | 桌面离地高为1.28m | B. | 桌面离地高为1.25m | ||
| C. | 物体经过0.4s后落地 | D. | 物体通过最后0.8m用时0.2s |
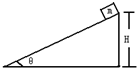 如图所示,质量为m=2kg物体由静止开始沿倾角为θ=37°的光滑斜面下滑,H=1.5m,求:
如图所示,质量为m=2kg物体由静止开始沿倾角为θ=37°的光滑斜面下滑,H=1.5m,求: