题目内容
8．一物体作直线运动的速度图象如图所示，则下列说法错误的是（ ）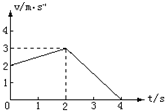
| A． | 前2s内做匀加速直线运动 | B． | 前4s内做匀变速直线运动 | ||
| C． | 前4s内的平均速度为2m/s | D． | 后2s内的加速度为-1.5m/s2 |
分析 v-t图象是速度时间图象，反映了物体的速度随时间的变化情况，倾斜的直线表示匀变速直线运动，根据图线与时间轴所围的面积求出位移，位移与时间之比即为平均速度，图线的斜率等于加速度．
解答 解：A、前2s内物体的速度均匀增大，做匀加速直线运动，故A正确．
B、前2s内和后2s内图线的斜率不同，则加速度不同，所以物体做的是非匀变速直线运动，故B错误．
C、根据速度图象与时间轴所围的面积表示位移，可得前4s内物体的位移为：x=$\frac{1}{2}$×2×（2+3）+$\frac{1}{2}$×2×3=8m，平均速度为：$\overline{v}$=$\frac{x}{t}$=$\frac{8}{4}$m/s=2m/s，故C正确．
D、速度图线的斜率等于加速度，则得：后2s内的加速度为 a=$\frac{0-3}{2}$m/s2=-1.5m/s2．故D正确．
本题选错误的，故选：B
点评 速度图象问题关键抓住两个数学意义：图线的斜率等于加速度、图线与时间轴所围的面积大小等于位移，即可分析其运动情况．
练习册系列答案
相关题目
16．雨滴落到窗台的速度为5m/s，经过窗户的速度是4m/s，那么（ ）
| A． | 5 m/s 是平均速度，4 m/s 是瞬时速度 | |
| B． | 5 m/s 是瞬时速度，4 m/s是平均速度 | |
| C． | 5 m/s和4 m/s都是平均速度 | |
| D． | 5 m/s和4 m/s都是瞬时速度 |
3．
如图所示，把一个带正电的小球放入原来不带电的金属空腔球壳内并接触，其结果可能是（ ）
如图所示，把一个带正电的小球放入原来不带电的金属空腔球壳内并接触，其结果可能是（ ）| A． | 球壳的内、外表面都带正电 | |
| B． | 只有球壳外表面带正电 | |
| C． | 球壳的内表面带正电，外表面带负电 | |
| D． | 球壳的内表面带负电，外表面带正电 |
1．
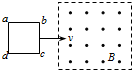一个闭合矩形线圈abcd以速度v从无磁场区域匀速穿过匀强磁场区域，而再次进入无磁场区域，如图所示，设感应电流沿顺时针方向为正值，那么，下图中能正确反映线圈中电流-时间关系的图象是（ ）
一个闭合矩形线圈abcd以速度v从无磁场区域匀速穿过匀强磁场区域，而再次进入无磁场区域，如图所示，设感应电流沿顺时针方向为正值，那么，下图中能正确反映线圈中电流-时间关系的图象是（ ）| A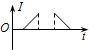． |  | B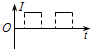． |  | C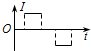． |  | D． |  |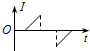
6．在做“研究匀变速直线运动”的实验时，某同学得到一条用电火花计时器打下的纸带如图1所示，并在其上取了A、B、C、D、E、F、G 7个计数点，每相邻两个计数点间还有4个点图中没有画出，电火花计时器接220V、50Hz交流电源．
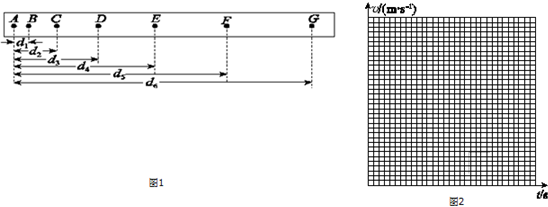
（1）电火花打点计时器每隔0.02打一次点，设电火花计时器的周期为T，计算F点的瞬时速度VF的公式为VF=$\frac{{d}_{6}-{d}_{4}}{2T}$（d4、d6和T表示）；
（2）实验过程中，下列做法正确的是AD．
A．先接通电源，再使纸带运动
B．先使纸带运动，再接通电源
C．将接好纸带的小车停在靠近滑轮处
D．将接好纸带的小车停在靠近打点计时器处
（3）他经过测量并计算得出电火花计时器在打B、C、D、E、F各点时物体的瞬时速度如下表．以A点对应的时刻为t=0，试在如图2所示坐标系中合理地选择标度，作出vt图象，并利用该图象求出物体的加速度a=0.40 m/s2；
（4）如果当时电网中交变电流的电压变成210V，而做实验的同学并不知道，那么加速度的测量值与实际值相比不变．（填“偏大”、“偏小”或“不变”）
（1）电火花打点计时器每隔0.02打一次点，设电火花计时器的周期为T，计算F点的瞬时速度VF的公式为VF=$\frac{{d}_{6}-{d}_{4}}{2T}$（d4、d6和T表示）；
（2）实验过程中，下列做法正确的是AD．
A．先接通电源，再使纸带运动
B．先使纸带运动，再接通电源
C．将接好纸带的小车停在靠近滑轮处
D．将接好纸带的小车停在靠近打点计时器处
（3）他经过测量并计算得出电火花计时器在打B、C、D、E、F各点时物体的瞬时速度如下表．以A点对应的时刻为t=0，试在如图2所示坐标系中合理地选择标度，作出vt图象，并利用该图象求出物体的加速度a=0.40 m/s2；
| 对应点 | B | C | D | E | F |
| 速度（m/s） | 0.141 | 0.180 | 0.218 | 0.262 | 0.301 |