题目内容
【题目】如图所示,质量为5.0kg的小车以2.0m/s的速度在光滑的水平面上向左运动,小车上AD部分是表面粗糙的水平轨道,DC部分是四分之一光滑圆弧轨道,整个轨道都是由绝缘材料制成的,小车所在空间内有竖直向上的匀强电场和垂直纸面向里的匀强磁场,电场强度大小E为50N/C,磁感应强度大小B为2.0T.现有一质量为2.0kg、带负电且电荷量为0.10C的滑块以10m/s向右滑入小车,当滑块运动到D点时相对地面的速度为向右的5.0m/s,计算结果保留两位有效数字,求:
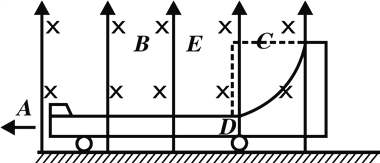
(1)滑块从A到D的过程中,小车、滑块组成的系统损失的机械能.
(2)如果滑块刚过D点时对轨道的压力为76N,求圆弧轨道的半径r.
(3)当滑块通过D点时,立即撤去磁场,要使滑块不冲出圆弧轨道,求此圆弧的最小半径.
【答案】(1)85J(2)1.0m(3)0.71m
【解析】(1)设滑块运动到D点时的速度大小为![]() ,小车在此时的速度大小为
,小车在此时的速度大小为![]() ,
,
滑块从A运动到D的过程中系统动量守恒,以向右为正方向,有:![]() ,代入数据解得
,代入数据解得![]() ;
;
则小车跟滑块组成的系统的初机械能![]() ,
,
小车跟滑块组成的系统的末机械能![]() ,
,
代入数据解得:![]() ,
,
小车与滑块组成的系统损失的机械能![]() ;
;
(2)设滑块刚过D点时,受到轨道的支持力为N,则由牛顿第三定律可得![]()
由牛顿第二定律可得![]() ,代入数据解得
,代入数据解得![]() ;
;
(3)设滑块沿圆弧轨道上升到最大高度时,滑块与小车具有共同的速度![]()
则由动量守恒定律可得![]() ,代入数据解得
,代入数据解得![]() ;
;
设圆弧轨道的最大半径为R,则由能量守恒关系,有![]()
代入数据解得:R=0.71m。

练习册系列答案
 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案
相关题目