题目内容
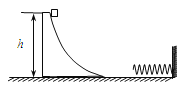
【题目】如图,轨道的水平部分粗糙,竖直的半圆部分光滑,半径R=0.32m。Q为轨道上最高点、P为最低点、T点与圆心等高。质量m=2kg的小滑块从水平轨道A点(图中未画出,且AP距离可调节)以v0=6m/s的初速度向右滑行。己知滑块与水平轨道间的动摩擦因数μ=0.2,g取10m/s2。
(1)求滑块能够通过Q点的最小速度VQ;
(2)若滑块恰好能滑到Q点,求滑块从A运动到P的时间t;
(3)若滑块在半圆轨道间不脱离轨道,求AP距离的取值范围。

【答案】(1)![]() (2)t=1s(3)l<5m或7.4m≤l<9m
(2)t=1s(3)l<5m或7.4m≤l<9m
【解析】
(1)根据牛顿第二定律可求滑到Q点时的最小速度;
(2)由机械能守恒可求到达P点的速度,由牛顿第二定律可求加速度,根据速度时间关系可求时间;
(3)若滑块在半圆轨道间不脱离轨道,根据刚好到达Q点、T点和P点,分别应用动能定理可求AP距离的取值范围。
(1)在Q点,由牛顿第二定律得
![]()
得![]()
(2)滑块从P到Q,由机械能守恒得
![]()
在水平轨道,由牛顿第二定律得
μmg=ma
![]()
得t=1s
(3)若滑块恰好到达Q点,由动能定理得
![]()
得![]()
如滑块恰好到达T点,由动能定理得
![]()
得![]()
如滑块恰好到达P点,由动能定理得
![]()
得![]()
所以AP距离![]() ;或
;或![]()

练习册系列答案
 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案
相关题目