题目内容
【题目】如图所示,用折射率n=![]() 的玻璃做成内径为R、外径为R'=
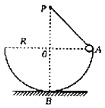
的玻璃做成内径为R、外径为R'=![]() R的半球形空心球壳,一束平行光射向此半球的外表面,且与中心对称轴OO′平行,不计多次反射。求球壳内部有光线射出的区域?(用与OO′所成夹角表示)
R的半球形空心球壳,一束平行光射向此半球的外表面,且与中心对称轴OO′平行,不计多次反射。求球壳内部有光线射出的区域?(用与OO′所成夹角表示)
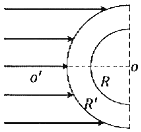
【答案】以OO'为中心线,上、下(左、右)各60°的圆锥球壳内均有光线射出。
【解析】
设光线a′a射入外球面,沿ab方向射向内球面,刚好发生全反射,则有:
sinC=![]()
可得C =45°
在△Oab中,Oa=![]() R,Ob=R
R,Ob=R
由正弦定理得![]() =
=![]()
解得:r=30°
由![]() =n,得i=45°
=n,得i=45°
又因为∠O′Oa=i,
∠θ=C-r=45°-30°=15°
所以∠O′Ob=i+θ=45°+15°=60°
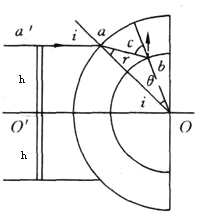
当射向外球面的入射光线的入射角小于i=45°时,这些光线都会射出内球面。因此,以OO'为中心线,上、下(左、右)各60°的圆锥球壳内均有光线射出。

练习册系列答案
 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案
相关题目