题目内容
【题目】（18分）
如图甲所示，倾角θ =37°的粗糙斜面固定在水平面上，斜面足够长。一根轻弹簧一端固定在斜面的底端，另一端与质量m=1.0kg的小滑块（可视为质点）接触，滑块与弹簧不相连，弹簧处于压缩状态。当t=0时释放滑块。在0~0.24s时间内，滑块的加速度a随时间t变化的关系如图乙所示。已知弹簧的劲度系数
N/m，当t=0.14s时，滑块的速度v1=2.0m/s。g取l0m/s2，sin37°=0.6，cos37°=0.8。弹簧弹性势能的表达式为
（式中k为弹簧的劲度系数，x为弹簧的形变量）。求：
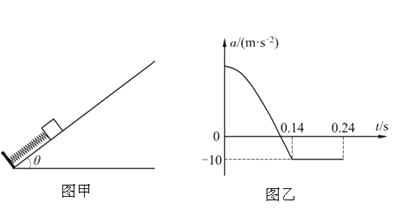
（1）斜面对滑块摩擦力的大小f；
（2）t=0.14s时滑块与出发点间的距离d；
（3）在0~0.44s时间内，摩擦力做的功W。
【答案】（1）4.0N；（2）0.20m；（3）－1.64J。
【解析】试题分析：（1）由题中的图乙可知，在t1=0.14s后这段过程中滑块加速度的大小a1=10m/s2。根据牛顿第二定律有：
（2分）
所以f="4.0N" （2分）
（2）当t1=0.14s时弹簧恰好恢复原长，在这段过程中，根据能的转化与守恒有
（2分）
其中
（1分）
（1分）
（1分）
联立可求得 d =" 0.20" m （1分）
（3）设从t1=0.14s时开始，经时间
滑块的速度减为零，则有
s （1分）
这段时间内滑块运动的距离
m （1分）
此时t2=0.14s+=0.34s （1分）
此后滑块将反向做匀加速直线运动，根据牛顿第二定律可求得此时加速度的大小
m/s2（2分）
在0.34s~0.44s（
s）时间内，滑块反向运动的距离
m （1分）
所以在0~0.44s时间内，摩擦力f做的功
J （2分）
练习册系列答案
期末100分闯关海淀考王系列答案
相关题目
