��Ŀ����
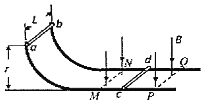
����Ŀ����ͼ�����ΪL�Ĺ⻬�������죬�뾶Ϊr��![]() Բ��������ֱ���á�ֱ�IJ��̶ֹ���ˮƽ���棬MNQP��Χ���дŸ�Ӧǿ�ȴ�СΪB��������ֱ���µ���ǿ�ų���������ab��cd��ֱ��������ҽӴ����ã�cd��ֹ�ڴų��У�ab��Բ������Ķ����ɾ�ֹ�ͷţ�����ų�����cd���˶���ʼ�ղ��Ӵ�����֪�����������������Ϊm�������ΪR������������費�ƣ��������ٶ�Ϊg����
Բ��������ֱ���á�ֱ�IJ��̶ֹ���ˮƽ���棬MNQP��Χ���дŸ�Ӧǿ�ȴ�СΪB��������ֱ���µ���ǿ�ų���������ab��cd��ֱ��������ҽӴ����ã�cd��ֹ�ڴų��У�ab��Բ������Ķ����ɾ�ֹ�ͷţ�����ų�����cd���˶���ʼ�ղ��Ӵ�����֪�����������������Ϊm�������ΪR������������費�ƣ��������ٶ�Ϊg����
��1��ab������Բ����ʱ�Թ��ѹ���Ĵ�С��
��2����ab���ٶ�Ϊ![]() ʱ��cd�����ٶȵĴ�С����ʱ������δ�뿪�ų���
ʱ��cd�����ٶȵĴ�С����ʱ������δ�뿪�ų���
��3����cd����![]() �뿪�ų�����֪��cd����ʼ�˶������뿪�ų�һ��ʱ���ͨ��cd���ĵ����Ϊq����˹���ϵͳ�����Ľ������Ƕ��١����˹���ab��ʼ���ڴų����˶���
�뿪�ų�����֪��cd����ʼ�˶������뿪�ų�һ��ʱ���ͨ��cd���ĵ����Ϊq����˹���ϵͳ�����Ľ������Ƕ��١����˹���ab��ʼ���ڴų����˶���
���𰸡���1��3mg����2��![]() ����3��BLq
����3��BLq![]() -
-![]() mgr-
mgr-![]() ��
��
��������
��1��ab�»����̻�е���غ㣬�ɻ�е���غ㶨�ɵã�mgr=![]() ��
��
��ã�v0=![]() ��
��
ab�˶�����ʱ����ţ�ٵڶ����ɵã�F-mg=m![]() ��
��
��ã�F=3mg��
��ţ�ٵ�������֪��ab�Թ��ѹ����С��F��=F=3mg��
��2��������ɵ�ϵͳ�����غ㣬������Ϊ������
�ɶ����غ㶨�ɣ�mv0=mvab+mv����
��ã�v��=![]() ��
��
ab�������ĵ綯�ƣ�Eab=BLvab��
cd�������ĸ�Ӧ�綯�ƣ�Ecd=BLv����
��·�е�����I=![]() ��
��
��ã�I=![]() ��
��
��ʱcd�����ܰ�������F=BIL��
��ʱcd�����ٶȣ�a=![]() ��
��
��ã�a=![]() ��
��
��3���������֪��cd����![]() �뿪�ų������������˶���
�뿪�ų������������˶���
�Ҵ�cd����ʼ�˶���ͨ��������Ϊq��ʱ���ڣ�ͨ��ab�������ҲΪq��
��ab�����ɶ���������֪��-B![]() Lt=mvab-mv0��
Lt=mvab-mv0��
����q=![]() t��
t��
��ã�vab=![]() -
-![]() ��
��
�˹��̣��������غ㶨�ɵã�mgr=![]() +Q��
+Q��
��ã�Q=BLq![]() -
-![]() mgr-
mgr-![]() ��
��