题目内容

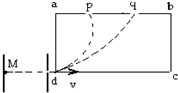
如图在矩形abcd区域内存在着匀强磁场，A、B带电粒子都是从M点由静止经同一电场加速后从顶角d处沿dc方向射入磁场，A、B又分别从p、q两处射出，已知dp连线和dq连线与ad边分别成30°和60°角，不计重力．A、B两粒子在磁场中运动的速度大小之比vA：vB为（　　）
A．VA：VB=2：1B．VA：VB=2：3C．VA：VB=3：1D．VA：VB=3：2

由几何关系得，p、q两点射出磁场的粒子做圆周运动的半径分别为RA=
2
3
ad，RB=2ad
即：RA：RB=1：3
由动能定理：qU=
1
2
mv2
洛伦兹力提供向心力：qvB=
mv2
R

故：v=
2U
RB

则：
vA
vB
=
RB
RA
=
3
1

故C正确，ABD错误

故选：C
练习册系列答案
相关题目
如图所示电路，电源电动势E=90V，内阻r=5Ω，R1=10Ω，R2=20Ω，板面水平放置的平行板电容器的两极板M、N相距d=3cm，在两板间的正中央有一带电液滴，电量q=2×10-7C，质量m=4×10-5kg，取g=10m/s2，求：
（1）若液滴恰好能处于静止状态，电压表的示数是多少？若此时滑动变阻器的滑动触头C正好在变阻器正中点，那么滑动变阻器的最大阻值Rm是多大？
（2）将滑动触头C迅速滑到A端，则液滴将向哪个极板作什么性质的运动？到达该极板时的速度是多大？
如图是示波管中的电子枪部分示意图．从灯丝K发射出的电子经过加速电压U的加速到达阳极B，电子的电荷为e，质量为m．电子从灯丝发射时的速度可看作为零，则加速电极的B极板应该接在电源的______极（填“+”或“-”）．电子到达B羁绊时的速度大小为______．
如图所示，有一质子（质量为m，电荷量为e）由静止开始经电压为U1的电场的加速后，进入两块板间距离为d、板间电压为U2的平行金属板间，若质子恰好从两板正中间垂直电场方向射入偏转电场，求：（不计质子的重力）
（1）质子进入偏转电场时的速度；
（2）为保证质子能从下极板正中央的小孔射出，则极板的长度应为多少？
A、B两金属板平行放置，在t=0时将电子从A板附近由静止释放，则在A、B两板间加上下列哪个电压时，有可能使电子到不了B板（　　）
A．B．C．D．
如图，水平放置的金属薄板A、B间有匀强电场，电场强度大小E=2.0×106N/C．A板上有一小孔，D为小孔正上方h=3.2cm处的一点．一带负电的油滴在重力G=3.2×10-12N作用下，由D点静止开始做自由落体运动．当油滴进入电场后，恰好做匀速直线运动．求：（g取10m/s2）
（1）油滴刚进入电场时的速度大小v；
（2）油滴所带的电荷量q；
（3）若A、B两板之间的距离为d=10cm，试求油滴从D运动到B板的总时间t．
如图，a、b、c、d是某匀强电场中的四个点，它们正好是一个矩形的四个顶点，ab=cd=L，ad=bc=2L，电场线与矩形所在平面平行．已知a点电势为20V，b点电势为24V，d点电势为12V．一个质子从b点以v0的速度射入此电场，入射方向与bc成45°，一段时间后经过c点．不计质子的重力．下列判断正确的是（　　）
A．c点电势为16V
B．场强的方向由b指向d
C．质子从b运动到c所用的时间为
2
L
v0
D．质子从b运动到c，电场力做功为8eV
一束初速度不计的电子流经加速电压U加速后，在距两极板等距处垂直进入平行板间的匀强电场，如图所示，若平行板间距离d=1.0cm，板长L=5.0cm，电子的质量和电荷量大小分别为m和e，电子的重力不计，问：
（1）电子离开加速电场时的速度v是多少？
（2）要使电子能从平行板间飞出，两个极板间能加的最大电压Um与加速电压U之比是多少？
在“练习使用示波器”的实验中，关于竖直位移旋钮和Y增益旋钮的作用，下列说法正确的是     (　　)．
A．竖直位移旋钮用来调节图像在竖直方向的位置，Y增益旋钮用来调节图像在竖直方向的幅度
B．竖直位移旋钮用来调节图像在竖直方向的幅度，Y增益旋钮用来调节图像在竖直方向的位置
C．竖直位移旋钮和Y增益旋钮都是用来调节图像在竖直方向的位置的
D．竖直位移旋钮和Y增益旋钮都是用来调节图像在竖直方向的幅度的

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网