题目内容
19. 足够长的平行金属轨道M,N,相距L=0.5m,且水平放置;M,N左端与半径R=0.4m的光滑竖直圆轨道相连,金属棒b和c可在轨道上无摩擦地滑动,两金属棒的质量mb=mc=0.1kg,电阻Rb=Rc=1Ω,轨道的电阻不计.平行水平金属轨道M,N处于磁感应强度B=1T的匀强磁场中,磁场方向与轨道平面垂直,光滑竖直圆轨道在磁场外,如图所示,若使b棒以初速度v0=10m/s开始向左运动,求:
足够长的平行金属轨道M,N,相距L=0.5m,且水平放置;M,N左端与半径R=0.4m的光滑竖直圆轨道相连,金属棒b和c可在轨道上无摩擦地滑动,两金属棒的质量mb=mc=0.1kg,电阻Rb=Rc=1Ω,轨道的电阻不计.平行水平金属轨道M,N处于磁感应强度B=1T的匀强磁场中,磁场方向与轨道平面垂直,光滑竖直圆轨道在磁场外,如图所示,若使b棒以初速度v0=10m/s开始向左运动,求:(1)c棒的最大速度;
(2)c棒中产生的焦耳热;
(3)若c棒达到最大速度后沿圆轨道上滑,求金属棒c达轨道最高点时对轨道的压力的大小.
分析 (1)根据动量守恒定律求解c棒的最大速度;
(2)根据能量守恒定律求解两棒中产生的总热量,再根据热量分配关系求解c棒中产生的焦耳热;
(3)由机械能守恒求解最高点的速度,在最高点由牛顿第二定律和牛顿第三定律解得在最高点C棒对轨道的压力.
解答 解:(1)在磁场力作用下,b棒做减速运动,c棒做加速运动,当两棒速度相等时,c棒达最大速度.
选两棒为研究对象,根据动量守恒定律有:mbvo=(mb+mc)v
解得c棒的最大速度为:v=$\frac{m_b}{{{m_b}+{m_c}}}$vo=$\frac{1}{2}$vo=5 m/s;
(2)从 b 棒开始运动到两棒速度相等的过程中,系统减少的动能转化为电能,两棒中产生的总热量为:Q=$\frac{1}{2}$mvo2-$\frac{1}{2}$(mb+mc)v2=2.5 J,
因为 Rb=Rc 所以 c 棒中产生的焦耳热为:Qc=$\frac{Q}{2}$=1.25 J;
(3)对c棒,沿圆轨道滑到最高点时的速度为v',上升到最高点的过程由机械能守恒可得:$\frac{1}{2}m{v^2}-\frac{1}{2}m{v'^2}=mg2R$,
解得v'=3m/s
最高点,设轨道对C棒的支持力为F,由牛顿第二定律得$mg+F=m\frac{{{{v'}^2}}}{R}$,
解得F=1.25N,
由牛顿第三定律得,在最高点C棒对轨道的压力为1.25N.
答:(1)c棒的最大速度为5 m/s;
(2)c棒中产生的焦耳热为1.25 J;
(3)若c棒达到最大速度后沿圆轨道上滑,金属棒c达轨道最高点时对轨道的压力的大小为1.25N.
点评 对于电磁感应问题研究思路常常有两条:一条从力的角度,重点是分析安培力作用下导体棒的平衡问题,根据平衡条件列出方程;另一条是能量,分析涉及电磁感应现象中的能量转化问题,根据动能定理、功能关系、动量守恒定律等列方程求解.

 阅读快车系列答案
阅读快车系列答案| A. | 据a=ω2r可知α∝r | B. | 据a=$\frac{{v}^{2}}{r}$可知a∝$\frac{1}{r}$ | ||
| C. | 据a=G$\frac{M}{{r}^{2}}$可知a∝$\frac{1}{{r}^{2}}$ | D. | 据a=ωv可知a与r无关 |
 如图所示,M、N两点分别放置两个等量异种电荷,A为它们连线的中点,B为连线上靠近N的一点,C为连线的中垂线上处于A点上方的一点,同一负电荷放在A、B、C三点时( )
如图所示,M、N两点分别放置两个等量异种电荷,A为它们连线的中点,B为连线上靠近N的一点,C为连线的中垂线上处于A点上方的一点,同一负电荷放在A、B、C三点时( )| A. | 放在A点受力最小,放在B点电势能最大 | |
| B. | 放在C点受力最小,放在B点电势能最小 | |
| C. | 放在B点受力最小,放在C点电势能最大 | |
| D. | 放在A点受力最大,放在C点电势能最大 |
 如图所示,虚线a、b、c代表电场中三个等势面,相邻等势面之间的电势差相等.实线为一带负电的粒子,仅在电场力作用下通过该区域时的运动轨迹,P、Q是这条轨迹上的两点,据此可知,下列说法中正确的是( )
如图所示,虚线a、b、c代表电场中三个等势面,相邻等势面之间的电势差相等.实线为一带负电的粒子,仅在电场力作用下通过该区域时的运动轨迹,P、Q是这条轨迹上的两点,据此可知,下列说法中正确的是( )| A. | 三个等势面中,c点的电势最高 | |
| B. | 粒子在P点的加速度方向沿着等势面a的切线方向 | |
| C. | 对于P、Q两点,带电粒子通过P点时电势能较大 | |
| D. | 由于不知道带电粒子运动的方向,无法比较P、Q两点的动能大小 |
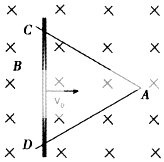 如图所示,光滑金属导轨AC、AD固定在水平面内,并处在方向竖直向下、大小为B的匀强磁场中.有一质量为m的导体棒以初速度V0从某位置开始在导轨上水平向右运动,最终恰好静止在A点.在运动过程中,导体棒与导轨始终构成等边三角形回路,且通过A点的总电荷量为Q.已知导体棒与导轨间的接触电阻值恒为R,其余电阻不计,则( )
如图所示,光滑金属导轨AC、AD固定在水平面内,并处在方向竖直向下、大小为B的匀强磁场中.有一质量为m的导体棒以初速度V0从某位置开始在导轨上水平向右运动,最终恰好静止在A点.在运动过程中,导体棒与导轨始终构成等边三角形回路,且通过A点的总电荷量为Q.已知导体棒与导轨间的接触电阻值恒为R,其余电阻不计,则( )| A. | 该过程中导体棒做匀减速运动 | |
| B. | 当导体棒的速度为$\frac{{v}_{0}}{2}$时,回路中感应电流小于初始时的一半 | |
| C. | 开始运动时,导体棒与导轨所构成回路的面积为S=$\frac{QR}{B}$ | |
| D. | 该过程中接触电阻产生的热量为$\frac{m{v}_{0}^{2}}{8}$ |
 如图所示,两个光滑绝缘的矩形斜面WRFE、HIFE对接在EF处,倾角分别为α=53°、β=37°.质量为m1=1kg的导体棒AG和质量为m2=0.5kg的导体棒通过跨过EF的柔软细轻导线相连,两导体棒均与EF平行、先用外力作用在AG上使它们静止于斜面上,两导体棒的总电阻为R=5Ω,不计导线的电阻.导体棒AG下方为边长L=1m的正方形区域MNQP有垂直于斜面向上的、磁感强度B1=5T的匀强磁场,矩形区域PQKS有垂直于斜面向上的、磁感强度B2=2T的匀强磁场,PQ平行于EF,PS足够长.已知细导线足够长,现撤去外力,导体棒AG进入磁场边界MN时恰好做匀速运动.(sin37°=0.6、sin53°=0.8,g=10m/s2,不计空气阻力.)求:
如图所示,两个光滑绝缘的矩形斜面WRFE、HIFE对接在EF处,倾角分别为α=53°、β=37°.质量为m1=1kg的导体棒AG和质量为m2=0.5kg的导体棒通过跨过EF的柔软细轻导线相连,两导体棒均与EF平行、先用外力作用在AG上使它们静止于斜面上,两导体棒的总电阻为R=5Ω,不计导线的电阻.导体棒AG下方为边长L=1m的正方形区域MNQP有垂直于斜面向上的、磁感强度B1=5T的匀强磁场,矩形区域PQKS有垂直于斜面向上的、磁感强度B2=2T的匀强磁场,PQ平行于EF,PS足够长.已知细导线足够长,现撤去外力,导体棒AG进入磁场边界MN时恰好做匀速运动.(sin37°=0.6、sin53°=0.8,g=10m/s2,不计空气阻力.)求: 我国将于2022年举办冬奥会,跳台滑雪是其中最具观赏性的项目之一.如图所示,质量m=60kg的运动员从长直助滑道AB的A处由静止开始,在无助力的情况下以加速度a=3.6m/s2匀加速滑下,到达B点时速度vB=24m/s,A与B的竖直高度差H=48m.为了改变运动员的运动方向,在助滑道与起跳台D点之间用一段弯曲滑道BCD衔接,B与C点的高度差h=5m,C与D点的高度差h′=4m,忽略BCD上的摩擦,g取10m/s2.求:
我国将于2022年举办冬奥会,跳台滑雪是其中最具观赏性的项目之一.如图所示,质量m=60kg的运动员从长直助滑道AB的A处由静止开始,在无助力的情况下以加速度a=3.6m/s2匀加速滑下,到达B点时速度vB=24m/s,A与B的竖直高度差H=48m.为了改变运动员的运动方向,在助滑道与起跳台D点之间用一段弯曲滑道BCD衔接,B与C点的高度差h=5m,C与D点的高度差h′=4m,忽略BCD上的摩擦,g取10m/s2.求: 如图所示,两平行金属导线MN、PQ固定在一绝缘水平面内,导轨电阻不计,间距为L,导轨平面处在一方向竖直向下的磁场中,两端M、P之间连接一阻值为R的定值电阻,质量为m、阻值为r的导体棒ab垂直导轨放置,且距MP端也为L,现对导体棒施加一水平外力,使之从静止开始以加速度a沿x轴的正方向运动,设棒的初始位置为坐标原点,平行导轨向右为x轴正方向,棒刚运动开始计时,试求:
如图所示,两平行金属导线MN、PQ固定在一绝缘水平面内,导轨电阻不计,间距为L,导轨平面处在一方向竖直向下的磁场中,两端M、P之间连接一阻值为R的定值电阻,质量为m、阻值为r的导体棒ab垂直导轨放置,且距MP端也为L,现对导体棒施加一水平外力,使之从静止开始以加速度a沿x轴的正方向运动,设棒的初始位置为坐标原点,平行导轨向右为x轴正方向,棒刚运动开始计时,试求: