题目内容
【题目】一质量M=2kg的长木板B静止在光滑的水平面上，B的右端与竖直挡板的距离为S=0.5m．一个质量为m=1kg的小物体A以初速度v0=6m/s从B的左端水平滑上B，当B与竖直挡板每次碰撞时，A都没有到达B的右端．
设定物体A可视为质点，A、B间的动摩擦因数μ=0.2，B与竖直挡板碰撞时间极短且碰撞过程中无机械能损失，g取10m/s2 ． 求：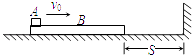
（1）B与竖直挡板第一次碰撞前的瞬间，A、B的速度值各是多少？
（2）最后要使A不从B上滑下，木板B的长度至少是多少？（最后结果保留三位有效数字．）
【答案】
（1）解：设A、B达到共同速度为v1时，B向右运动距离为S1
由动量守恒定律有：mv0=（M+m）v1
由动能定理有： 
联立解得：S1=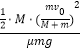 
= 
m=2m
由于S=0.5m＜2m，可知B与挡板碰撞时，A、B还未达到共同速度．设B与挡板碰撞前瞬间A的速度为vA，B的速度为vB，则
由动量守恒定律有：mv0=mvA+MvB
由动能定理有： 
联立解得：vA=4m/s、vB=1m/s
答：B与竖直挡板第一次碰撞前的瞬间，A、B的速度值分别是4m/s、1m/s．
（2）解：B与挡板第一次碰后向左减速运动，当B速度减为零时，B向左运动的距离设为SB，由动能定理有： 
由上式解得：SB=0.5m
在A的作用下B再次反向向右运动，设当A、B向右运动达到共同速度v2时B向右运动距离为S2，由动量守恒定律有：mvA﹣MvB=（M+m）v2
由动能定理有： 
解得： 
、 
故A、B以共同速度 
向右运动，B第二次与挡板碰撞后，以原速率反弹向左运动．此后由于系统的总动量向左，故最后A、B将以共同速度v3向左匀速运动．
由动量守恒定律有：（M﹣m）v2=（M+m）v3
解得： 
设A在B上运动的总量程为L（即木板B的最小长度），由系统功能关系得： 
代入数据解得：L=8.96m
答：最后要使A不从B上滑下，木板B的长度至少是8.96m．
【解析】（1）A在B上滑动时，以AB整体为研究对象可知，AB组成的系统动量守恒，由此可以求出AB速度相等时的速度；对B，运用动能定理可求出此过程滑行的位移，即可判断出B与挡板碰撞时，A、B还未达到共同速度．再对系统运用动量守恒和对B运用动能定理分别列式，即可求得B与竖直挡板第一次碰撞前的瞬间A、B的速度值．（2）B与挡板第一次碰后向左减速运动，由动能定理可求得向左运动的最大距离．在A的作用下B再次反向向右运动，可达到共同速度，由系统的动量守恒求出共同速度．当B第二次与挡板碰撞后，B的速度立即反向，而A将继续向右运动，此后由于系统的总动量向左，最后A、B将以共同速度v3向左匀速运动．再运用动量守恒和能量守恒求出A在B上运动的总路程，就是木板B最小的长度．
【考点精析】解答此题的关键在于理解动能定理的综合应用的相关知识，掌握应用动能定理只考虑初、末状态，没有守恒条件的限制，也不受力的性质和物理过程的变化的影响.所以，凡涉及力和位移，而不涉及力的作用时间的动力学问题，都可以用动能定理分析和解答，而且一般都比用牛顿运动定律和机械能守恒定律简捷，以及对动量守恒定律的理解，了解动量守恒定律成立的条件：系统不受外力或系统所受外力的合力为零；系统所受的外力的合力虽不为零，但系统外力比内力小得多；系统所受外力的合力虽不为零，但在某个方向上的分量为零，则在该方向上系统的总动量的分量保持不变．
