题目内容
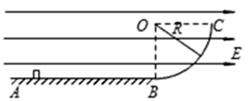
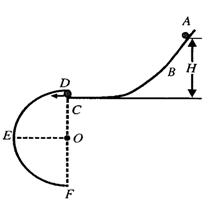
如图甲所示，一竖直平面内的轨道由粗糙斜面AD和光滑圆轨道DCE组成，AD与DCE相切于D点，C为圆轨道的最低点，将一小物块置于轨道ADC上离地面高为H处由静止下滑，用力传感器测出其经过C点时对轨道的压力N，改变H的大小，可测出相应的N的大小，N随H的变化关系如图乙折线PQI所示（PQ与QI两直线相连接于Q点），QI反向延长交纵轴于F点（0，5.8N），重力加速度g取10m／s2，求：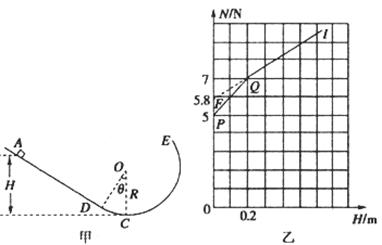
（1）小物块的质量m；
（2）小物块与斜面AD间的动摩擦因数μ。
（1）0.5kg；（2） 0.3
解析试题分析：(1)当H=0时，由图象的P点知：N=mg=5N m=0.5kg
(2)当物块从D点静止下滑，由图象PQ可知，h=0.2m，N1=7N
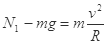；解得R=1m
，
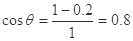如果物块由斜面上高H处静止滑下，
mgH－μmgcosθ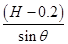
＝
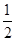mv22
N2－mg＝mv22/R
由FQI图象的F点知
当H＝0时，N2＝5.8 （图象中别的点也可）
代入，解得μ＝0.3.
考点：动能定理、圆周运动等。
练习册系列答案
相关题目
探究能力是物理学研究的重要能力之一，物体因绕轴转动而具有的动能叫转动动能，转动动能的大小与物体转动的角速度有关，为了研究砂轮的转动动能Ek与角速度ω的关系，某同学采用了下述实验方法进行探究：先让砂轮由动力带动匀速旋转，测得其角速度ω，然后让砂轮脱离动力，由于克服转轴间摩擦力做功，砂轮最后停下，测出砂轮脱离动力到停止转动的圈数n，通过分析实验数据，得出结论。经实验测得的几组ω和n如下表所示：
| ω/rad?s-1 | 0.5 | 1 | 2 | 3 | 4 |
| n | 5.0 | 20 | 80 | 180 | 320 |
| Ek/J | | | | | |
另外已测得砂轮转轴的直径为1 cm，转轴间的摩擦力为
（1）计算出砂轮每次脱离动力的转动动能，并填入上表中。
（2）由上述数据推导出砂轮转动动能与角速度的关系式为________________。
