题目内容
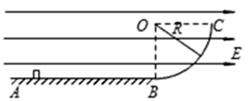
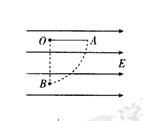
(10分)在水平向右的匀强电场中,有一质量为m、带正电的小球,用长为L的绝缘细线悬挂于O点,当小球处于A点时静止,细线与竖直方向夹角为a(如图所示),现在A点给小球一个垂直于悬线的初速度v0,使小球恰能在竖直平面内做圆周运动,求: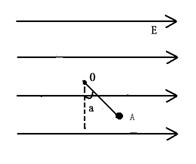
(1)在A点给小球的初速度v0多大?
(2)此过程中小球所受的最大拉力与最小拉力之差为多大?
(1)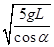 (2)
(2)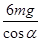
解析试题分析:如图所示,重力与电场力的合力:F=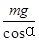 ,电场力为mgtanθ小球恰好做圆周运动,由牛顿第二定律得:
,电场力为mgtanθ小球恰好做圆周运动,由牛顿第二定律得: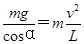 ,小球的最小速度
,小球的最小速度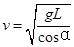 ,
,
由动能定理-mg×2Lcosα-mgtanα×2Lsinα=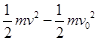 解得
解得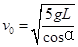 。重力与电场力的合力看作等效重力F=
。重力与电场力的合力看作等效重力F=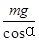 。在等效最高点处,T1+F=
。在等效最高点处,T1+F=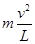 ,在等效最低点处T2-F=
,在等效最低点处T2-F=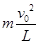 ,解得:T2-T1=
,解得:T2-T1=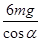
考点:本题考查动能定理及向心力来源。

练习册系列答案
 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案
相关题目
 。战机从A点开始滑跑,C点离舰,此过程中发动机的推力和飞机所受甲板和空气阻力的合力大小恒为F,ABC甲板总长度为L,战斗机质量为m,离舰时的速度为vm,不计飞机在B处的机械能损失。求AB部分的长度。
。战机从A点开始滑跑,C点离舰,此过程中发动机的推力和飞机所受甲板和空气阻力的合力大小恒为F,ABC甲板总长度为L,战斗机质量为m,离舰时的速度为vm,不计飞机在B处的机械能损失。求AB部分的长度。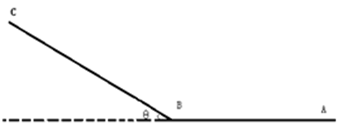
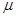 倍。开始时两球间距、球2与洞口间距均为L。求:
倍。开始时两球间距、球2与洞口间距均为L。求:
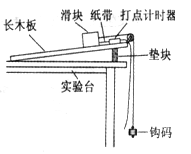

 和
和 ,1、3两点之间距离为s,重力加速度为g,探究结果的表达式是。(用相应的符号表示)
,1、3两点之间距离为s,重力加速度为g,探究结果的表达式是。(用相应的符号表示)