题目内容
1. 如图所示,在光滑绝缘水平面上,有一半径r=10cm、电阻R=0.01Ω、质量m=0.02kg的金属圆环以v0=10m/s的速度向一足够大、磁感应强度B=0.3T的匀强磁场滑去,当圆环刚好有一半进入磁场时,圆环的加速度为a=158.4m/s2.求此过程圆环增加的内能.
如图所示,在光滑绝缘水平面上,有一半径r=10cm、电阻R=0.01Ω、质量m=0.02kg的金属圆环以v0=10m/s的速度向一足够大、磁感应强度B=0.3T的匀强磁场滑去,当圆环刚好有一半进入磁场时,圆环的加速度为a=158.4m/s2.求此过程圆环增加的内能.
分析 根据切割产生的感应电动势公式求出感应电动势的大小,从而根据闭合电路欧姆定律求出电流的大小,再根据安培力大小公式求出安培力的大小,通过此时的安培力,结合牛顿第二定律求出加速度的大小与环的速度的大小之间的关系.最后根据能量守恒定律,抓住动能的减小量全部转化为热量求出.
解答 解:设圆环一半进入磁场时的速度为v
I=$\frac{E}{R}$=$\frac{B•2r•v}{R}$
此时受到的安培力F=BIL=$\frac{{4B}^{2}{r}^{2}v}{R}$
由牛顿第二定律可得:
环的加速度a=$\frac{F}{m}$=$\frac{2BIr}{m}$=$\frac{4{B}^{2}{r}^{2}v}{mR}$
解得:v=$\frac{maR}{4{B}^{2}{r}^{2}}$=$\frac{0.02×158.4×0.01}{4×0.{3}^{2}×0.{1}^{2}}$=8.8m/s
根据功能关系可得,环增加的内能△E=$\frac{1}{2}$mv02-$\frac{1}{2}$mv2
代入数据解得:
△E=0.23J.
答:此过程圆环增加的内能为0.23J.
点评 本题考查了电磁感应与电路、能量和力学的基本综合问题,要注意明确在圆环一半进入磁场时,切割长度为2r,同时掌握感应电动势、欧姆定律以及安培力公式的正确应用即可求解.

练习册系列答案
相关题目
12.下列描述中正确的是( )
| A. | 空气的相对湿度用空气中所含水蒸气的压强表示 | |
| B. | 随着分子间距增大,分子间引力和斥力均减小,分子势能不一定减小 | |
| C. | 布朗运动是由液体或气体分子从各个方向对悬浮粒子撞击作用的不平衡引起的 | |
| D. | 液体与大气相接触时,表面层内分子所受其他分子的作用表现为相互吸引 | |
| E. | 尽管技术不断进步,热机的效率仍不能达到100%,制冷机却可以使温度降到-293°C |
10.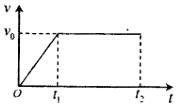 把一小物块轻轻放在一水平匀速运动的传送带的一端,物块一直运动到皮带另一端,其运动图象如图所示,图中所标的时间和速度以及重力加速度均为己知.下列说法正确的是( )
把一小物块轻轻放在一水平匀速运动的传送带的一端,物块一直运动到皮带另一端,其运动图象如图所示,图中所标的时间和速度以及重力加速度均为己知.下列说法正确的是( )
 把一小物块轻轻放在一水平匀速运动的传送带的一端,物块一直运动到皮带另一端,其运动图象如图所示,图中所标的时间和速度以及重力加速度均为己知.下列说法正确的是( )
把一小物块轻轻放在一水平匀速运动的传送带的一端,物块一直运动到皮带另一端,其运动图象如图所示,图中所标的时间和速度以及重力加速度均为己知.下列说法正确的是( )| A. | 物块先受滑动摩擦力作用,后受静摩擦力作用 | |
| B. | 由图中的数据可求出皮带的长 | |
| C. | 由图中的数据可求出因摩擦产生的热量 | |
| D. | 由图中的数据可求出物块与皮带间的动摩擦因数 |
11.某点电荷和金属圆环间的电场线分布如图所示.下列说法正确的是( )


| A. | a 点的电势高于 b 点的电势 | |
| B. | 若将一正试探电荷由 a 点移到 b 点,电场力做负功 | |
| C. | c 点的电场强度与 d 点的电场强度大小无法判断 | |
| D. | 若将一正试探电荷从 d 点由静止释放,电荷将沿着电场线由 d 到 c |
8.以下关于波的认识,哪些是不正确的( )
| A. | 潜艇利用声呐探测周围物体的分布情况,用的是波的反射原理 | |
| B. | 隐形飞机怪异的外形及表面涂特殊隐形物质,是为了减少波的反射,从而达到隐形的目的 | |
| C. | 雷达的工作原理是利用波的折射 | |
| D. | 水波从深水区传到浅水区改变传播方向的现象,是波的折射现象 |
8. 如图所示,在竖直平面内固定一圆心为O、半径为R的光滑圆环,原长为R的轻弹簧上端固定在圆环的最高点A,下端系有一个套在环上且重为G的小球P(可视为质点).若小球静止时,O、P两点的连线恰好水平,且弹簧的形变未超出其弹性限度,则弹簧的劲度系数为( )
如图所示,在竖直平面内固定一圆心为O、半径为R的光滑圆环,原长为R的轻弹簧上端固定在圆环的最高点A,下端系有一个套在环上且重为G的小球P(可视为质点).若小球静止时,O、P两点的连线恰好水平,且弹簧的形变未超出其弹性限度,则弹簧的劲度系数为( )
 如图所示,在竖直平面内固定一圆心为O、半径为R的光滑圆环,原长为R的轻弹簧上端固定在圆环的最高点A,下端系有一个套在环上且重为G的小球P(可视为质点).若小球静止时,O、P两点的连线恰好水平,且弹簧的形变未超出其弹性限度,则弹簧的劲度系数为( )
如图所示,在竖直平面内固定一圆心为O、半径为R的光滑圆环,原长为R的轻弹簧上端固定在圆环的最高点A,下端系有一个套在环上且重为G的小球P(可视为质点).若小球静止时,O、P两点的连线恰好水平,且弹簧的形变未超出其弹性限度,则弹簧的劲度系数为( )| A. | $\frac{G}{R}$ | B. | $\frac{G}{\sqrt{2}R}$ | C. | $\frac{(2+\sqrt{2})G}{R}$ | D. | $\frac{(2-\sqrt{2})G}{R}$ |

 ,此时恰好由一辆自行车(可视为质点)从火车头旁边同方向驶过,自行车速度
,此时恰好由一辆自行车(可视为质点)从火车头旁边同方向驶过,自行车速度 ,火车长
,火车长 。求:
。求: 和
和 的面积分别为
的面积分别为 和
和 (
( ),初始时,甲车在乙车前方
),初始时,甲车在乙车前方 处,那么
处,那么
 ,两车不会相遇
,两车不会相遇 ,两车相遇2次
,两车相遇2次 ,两车相遇1次
,两车相遇1次 ,两车相遇1次
,两车相遇1次